Эллипсометрия

ЭЛЛИПСОМЕТРИЯ, метод исследования св-в границы (пов-сти) раздела разл. сред и происходящих на ней явлений (адсорбция, окисление и др.) по параметрам эллиптич. поляризации отраженного света.
При отражении монохроматич. плоскополяризов. света, падающего под углом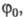 электромагн. волна, взаимодействуя с в-вом, обычно преобразуется в эллиптически поляризованную. Это объясняется тем, что электромагн. колебания, совершающиеся в плоскости падения (р-колебания) светового луча и в перпендикулярной к ней плоскости (s-колебания), при отражении света по-разному изменяют амплитуду напряженности электрич. поля Е и начальную фазу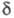 колебаний (рис.). Параметрами Е и 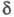характеризуются т. наз. комплексные амплитуды для р- и s-колебаний падающей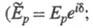 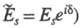и отраженной 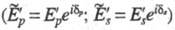волн. Отношения амплитуд 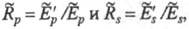или комплексные коэф. отражения, можно вычислить в рамках конкретной модели отражающей пов-сти, используя мат. аппарат теории комплексных чисел и электромагн. теорию света.

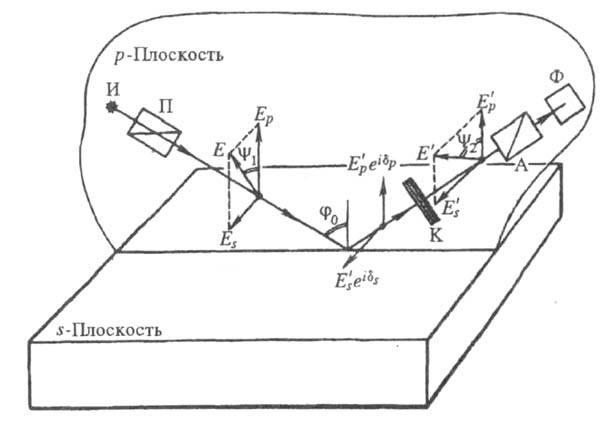
Схема действия эллипсометра; пояснения в тексте.

Такой подход, наз. прямой задачей Э., позволяет записать осн. ур-ние Э.:

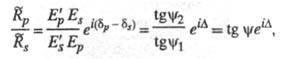
где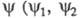 - соотв. для падающей и отраженной волн) и 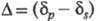- эллипсометрич. углы, измеряемые с помощью спец. приборов - эллипсометров.
В простейшей схеме эллипсометра, приведенной на рис., монохроматич. свет от источника И, проходя через призму-поляризатор П, преобразуется в плоскополяризов. свет. При отражении от исследуемой пов-сти между р- и s-колеба-ниями возникает разность фаз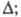 при этом конец вектора напряженности, характеризующего результирующее электрич. колебание, описывает эллипс. Компенсатор К приводит разность фаз между р- и s-колебаниями к нулю и снова преобразует свет в плоскополяризованный, к-рый можно полностью погасить анализатором А. Гашение фиксируется фотоприемником Ф. Значения азимутов поляризатора и анализатора в положении гашения связаны с углам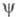ии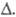
Прямая задача Э. легко решается для геометрически плоской границы раздела полубесконечных сред; разработаны методы решения для более сложных систем, напр., для планарной многослойной системы тонких пленок заданной толщины с известными оптич. постоянными сред. Совпадение вычисленных значени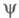й и с экспериментальными свидетельствует о корректности выбранной оптич. модели.
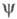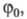Однако, как правило, необходимо решать обратную задачу Э.- находить оптич. характеристики отражающей системы по измеренному набору значений и при разных условиях: разл. углах падения света падении света на изучаемую пов-сть из разных сред, использование света разл. частот (т. наз. спектральная Э.).
С помощью прямых вычислений обратная задача м. б. решена для случая отражения света от идеальной (резкой, гладкой) плоской границы раздела; в частности, по измеренным эллипсометрич. углам можно рассчитать оптич. константы (показатели преломления и поглощения) металлов. При этом даже для хорошо отполированной металлич. пов-сти модель идеальной границы раздела не всегда корректна, поэтому следует учитывать шероховатость реальной пов-сти. Общего решения обратной задачи не существует. Оптич. характеристики находят посредством номограмм, построенных по результатам решения прямой задачи на ЭВМ или с помощью спец. программ типа "поиск".
Классич. область применения Э. - исследования оптич. св-в материалов, в т. ч. измерения оптич. постоянных тонких (напр., оксидных) пленок, а также их толщин. Интерес к Э. возрос в 70-80-х гг. 20 в. в связи с особым значением, к-рое приобрели анализ структуры, изучение физ.-хим. св-в и контроль чистоты пов-стей благодаря быстрому развитию твердотельной (прежде всего полупроводниковой) электроники. Э. используют также в исследованиях физ. и хим. адсорбции в глубоком вакууме на плоских пов-стях Si, Ag, Pt и др., адсорбции полимеров на границе жидкость-газ и жидкость-жидкость, процессов катализа на микроуровне, св-в верх. слоев пов-стей, подвергнутых коррозии, в электрохимии для изучения окисления и восстановления электродов, в микробиологии для исследования оболочек клеток и липидных мембран и др.
Достоинства Э.: простота и быстрота измерений (имеются автоматич. эллипсометры), возможность производить их в ходе процесса (in situ), в вакууме, при высоких т-рах, в агрессивных средах; кроме того, при экспериментах пов-сти не загрязняются и не разрушаются. Недостаток метода -трудность правильного выбора модели отражающей системы и интерпретации результатов измерений. Поэтому наиб. перспективно сочетание Э. с др. методами исследования пов-сти, напр. с оже-спектроскопией, УФ и рентгеновской спектроскопией, методами дифракции электронов и рассеяния ионов.

Лит.: Основы эллипсометрии, под ред. А. В. Ржанова, Новосиб., 1979; Аззам Р., Башара Н., Эллипсометрия и поляризованный свет, пер. с англ., М., 1981; Громов В. К., Введение в эллипсометрию, Л., 1986; Пшеницын В. И., Абаев М. И., Лызлов Н. Ю., Эллипсометрия в физико-химических исследованиях, Л., 1986; Всесоюзные конференции по эллипсометрии. Сб. тр., Новосиб., 1980-91; Эллипсометрия. Теория, методы, приложения, ред. К. К. Свиташев, А. С. Мардежов, Новосиб., 1991.

3. М. Зорин.