Столкновений теория

СТОЛКНОВЕНИЙ ТЕОРИЯ, простейший вариант теории газофазных химических р-ций, трактующий скорость р-дии как ф-цию частоты столкновений молекул, их концентраций, нек-рой пороговой энергии и т-ры. Предложена У. Мак-Льюисом, М. Поляни, К. Герцфельдом в 20-х гг. 20 в.

Мол. столкновения рассматриваются как столкновения бесструктурных частиц, имеющих точно установленную скорость, а часто и находящихся в строго определенных квантовых состояниях. Никакие внеш. силы, за исключением сил межмол. взаимодействия, не учитываются. Столкновения делят на упругие и неупругие. При упругом столкновении направления движения сталкивающихся частиц изменяются, а их суммарная кинетич. энергия сохраняется, перераспределяясь между частицами. В результате неупругого столкновения претерпевает изменение внутр. энергия сталкивающихся частиц и, следовательно, их полная кинетич. энергия. При этом изменяется квантовое состояние одной из сталкивающихся частиц либо обеих. Вероятность перехода системы из двух сталкивающихся частиц в результате их упругого или неупругого соударения в определенное конечное состояние характеризуется сечением соударения (сечением рассеяния) s, или эффективным сечением. Последнее имеет размерность площади и равно отношению частоты соударений Z (число столкновений за 1 с в 1 см³) к плотности потока рассеиваемых частиц, т.е. к числу частиц, проходящих в единицу времени через единичную площадку, нормальную к их скорости: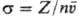 ("-концентрация частиц, 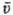-средняя скорость). Средняя скорость частиц м. б. определена, если известна ф-ция распределения частиц по скоростям. Для идеального газа в состоянии статистич. равновесия эта ф-ция представляет собой распределение Максвелла (см. Статистическая термодинамика).

Упругие столкновения молекул определяют явления переноса в газах: диффузию (перенос частиц), вязкость (перенос импульса), теплопроводность (перенос энергии). Соответствующие коэф. переноса определяются эффективными сечениями упругого рассеяния частиц. Сечение рассеяния атомов или молекул на большие углы наз. газокинетич. сечением; оно составляет по порядку величины 10^-15 см². Подвижность ионов в газовой фазе также связана с сечением рассеяния иона на атоме или молекуле (см. Ионы в газах). Неупругие столкновения могут приводить к разл. процессам: переходам между электронными, колебат. или вращат. состояниями молекул, ионизации, диссоциации, разл. хим. р-циям между частицами и др.; каждый из этих процессов характеризуется соответствующим сечением. Напр., столкновение двух молекул А и В, приводящее к хим. р-ции с образованием продуктов С и D, рассматривают с учетом квантовых состояний исходных молекул (обозначаются индексами i, j) и продуктов (индексы k, l) (см. Динамика элементарного акта). Процесс характеризуют детальным сечением взаимодействия s_kl/ij, пропорциональным потоку частиц продуктов C_k, D_l, в заданном направлении; величина сечения взаимод. зависит от кинетич. энергии взаимод. и начальных квантовых состояний частиц А_i и В_j и м. б. измерена, напр., с помощью молекулярных пучков метода.

С. т. рассматривает хим. р-цию, по существу, как результат столкновения молекул реагентов, в соответствии с представлениями кинетич. теории газов, осн. допущения к-рой сводятся к следующему: 1) молекулы-твердые бесструктурные сферы диаметром d; 2) в промежутках между столкновениями молекулы не взаимод. друг с другом; 3) время столкновения (контакта) пренебрежимо мало по сравнению со средним временем своб. пробега молекул между столкновениями (см. Газы). Число столкновений Z_AB молекул А и В в единицу времени в единице объема равно:

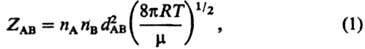
где n_А, n_в- концентрации молекул А и В (число соответствующих молекул в единице объема), d_АВ = 1/2(d_A + d_B)-средний диаметр сталкивающихся молекул, m = m_A m_B/(m_A + + m_B)-приведенная масса молекул А и В, R-газовая постоянная, Т-абс. т-ра.

Согласно С. т., не все столкновения приводят к химической р-ции. Энергией, вызывающей р-цию, является та часть полной кинетической энергии двух сталкивающихся молекул, к-рая соответствует компоненте относительной скорости двух молекул, направленной вдоль линии, соединяющей их центры в момент столкновения. Для протекания р-ции кинетическая энергия относительного движения А и В при столкновении должна превышать нек-рое критическое значение Е_кр (пороговая энергия). Доля молекул с энергией, превышающей Е_кр, определяется в основном множителем (Е_кр/RT+ 1) ехр (-Е_кр/RT). Т. обр., скорость р-ции iv представляет собой произведение частоты столкновений Z_AB на долю молекул, имеющих энергию, большую или равную Е_кр:

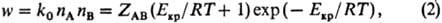
где k₀- константа скорости р-ции. Из (1) и (2) следует:

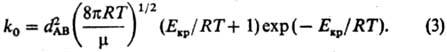
Температурная зависимость предэкспоненц. множителя приводит к нарушению аррениусовской температурной зависимости константы скорости (см. Аррениуса уравнение). Однако это нарушение незначительно, особенно при Е_кр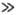RT.

Результаты расчетов констант скорости р-ций по выражению (3), как правило, значительно превышают измеренные значения, в связи с чем в выражение для константы скорости k вводят т. наз. стерич. фактор (вероятностный множитель) S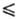1:

По существу, стерич. фактор-мера различия экспериментального и рассчитываемого по С. т. значений константы скорости; он составляет от 1 до 10^-5 для большинства р-ций.

В случае мономолекулярных превращений С. т. изучает в осн. закономерности перераспределения энергии изолир. молекулы по степеням свободы. Для бимолекулярных р-ций С.т. не позволяет определить константу скорости, т.к. нельзя рассчитать пороговую энергию и стерический фактор. Тем не менее С. т. сыграла важную роль в развитии представлений химической кинетики. В частности, она послужила базой при разработке активированного комплекса теории.

Осн. постулат этой теории состоит в том, что р-ция характеризуется переходом начальной конфигурации атомов при непрерывном изменении координат соответствующих ядер и электронов в конечную конфигурацию через нек-рую промежут. конфигурацию, к-рая является критич. для данной р-ции и соответствует высшей точке наиб. выгодного пути р-ции на поверхности потенциальной энергии. Результаты расчетов констант скорости р-ций по теории активир. комплекса совпадают со значениями, получаемыми по С. т., лишь для р-ций между атомами и простейшими молекулами (напр., I₂, Н₂). Для р-ций более сложных молекул С. т. неприменима, т.к. рассматривает сталкивающиеся молекулы как бесструктурные частицы, не имеющие внутр. степеней свободы.

Понятия С. т. используются в теории р-ций, скорость к-рых определяется диффузионным сближением реагирующих частиц (см. Диффузионно-контролируемые реакции, Реакции в растворах).

Лит. см. при ст. Кинетика химическая. А. А. Овсянников.