Скорость реакции

СКОРОСТЬ РЕАКЦИИ, скорость хим. превращения исходных в-в в продукты р-ции. В случае гомог. элементарной р-ции v_AA + v_BB : v_VV + v_ZZ, где V_A, V_B, v_V и V_Z-сте-хиометрич. коэф. реагентов А и В и продуктов V и Z соотв., в замкнутом постоянном объеме V реагент А исчезает со скоростью u_А = — d[А]/dt(t-время), а продукт Z появляется со скоростью u_Z = d[Z]/dt. С.р. определяется выражением:

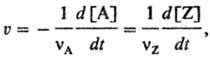
т. е. не зависит от того, по какому реагенту или продукту ее измеряют. Если в ходе р-ции изменяется объем V системы, v измеряют по изменению концентрации одного из в-в:

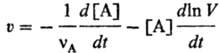
При постоянном объеме за протеканием р-ции можно следить, измеряя число молей n_А прореагировавшего в-ва и определяя глубину протыкания р-ции Dx = Dn_А/v_А; в этом случае

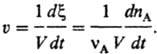
Для сложной р-ции (т.е. состоящей из ряда отдельно не наблюдаемых элементарных стадий) описание С. р. исходит из непосредственно определяемых хим. анализом или к.-л. другим способом изменений кол-в в-в. Наиб. просто С. р., протекающей стационарно, определяют в проточном безградиентном реакторе, в к-ром концентрации в-в и т-ра одинаковы по всему реакц. пространству (напр., благодаря перемешиванию или рециркуляции). В указанных условиях С. р. по в-ву В_m (m-номер в-ва) определяется выражением u_Bm = n_Bm/tV, где n_Bm-число молей в-ва В_m, образовавшегося за время г в реакц. объеме V, если р-ция гомогенна, или на пов-сти площадью f, если она гетерогенна (если В_m- исходное в-во, n_Bm < 0). В общем случае С. р. u_Bm различна в разных участках пространства и изменяется со временем, для ее определения пользуются соотношением:

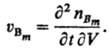
Скорости образования (расходования) всех в-в, участвующих в р-ции, взаимосвязаны. Если р-ция описывается одним хим. ур-нием 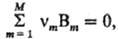к-рое представляет собой выражение закона сохранения в-ва (М-общее число реагентов и продуктов), С. р. по каждому в-ву u_Bm пропорциональна его стехиометрич. коэф. v_m (положительному для исходных в-в):

u_Bm=v_mu

Одинаковое для всех участвующих в р-ции в-в отношение u_Bm/v_m=u есть, по определению, С. р.

Если стехиометрия р-ции описывается неск. хим. ур-ниями, к-рые линейно независимы, т.е. любое др. хим. ур-ние является их линейной комбинацией, эти ур-ния полностью задают стехиометрию р-ции, их можно считать базисными. Число Q базисных ур-ний связано с числом М всех в-в в системе и числом с независимых компонентов, изменения масс к-рых выражают все возможные изменения в составе системы (см. Многокомпонентные системы) соотношением:

Q = М - с.

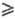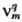Природой р-ции однозначно определено только число Q базисных ур-ний, выбор их м. б. сделан по-разному (Q следует отличать от числа P базисных маршрутов сложной р-ции-понятия, относящегося к механизму, а не к стехиометрии р-ции; всегда PQ). Пусть р-ция описывается Q базисными хим. ур-ниями где-стехиометрич. коэффициент в-ва В_m в 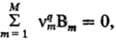ур-нии номер q (положит., отрицат. или равный нулю).

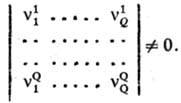
С. р. может быть охарактеризована скоростями образования т. наз. ключевых в-в B₁, B₂, ..., B_Q, для к-рых определитель, составленный из соответствующих стехиометрич. коэф., отличен от нуля:

Скорости образования всех в-в, участвующих в р-ции,-линейные ф-ции стехиометрич. коэффициентов :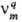

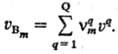
Зная u^q, посредством этой системы ур-ний получаем скорости образования остальных (М — Q)в-в. Величины u^(q) естественно считать С. р. по соответствующим хим. ур-ниям. Но следует при этом учитывать, что они имеют определенное значение лишь применительно ко всей данной совокупности базисных хим. ур-ний р-ции.

Для практич. целей скорости образования в-в при гетерог. катализе обычно относят не к единице пов-сти катализатора, а к массе или к объему слоя каталитич. зерен.

Приведенные определения отвечают общепринятому в хим. кинетике пониманию С. р. как интенсивной величины. Иногда, по преимуществу в литературе по хим. термодинамике, используют предложенное де Донде определение С.р., согласно к-рому она служит экстенсивной величиной. Для р-ции, описываемой одним хим. ур-нием, С. р.

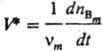
Экстенсивную величину V* удобнее называть производительностью (реактора, зерна катализатора, в зависимости от рассматриваемой зоны р-ции). Тогда С. р. v -плотность производительности или, в случае гетерог. р-ции, поверхностная плотность производительности. М. И. Темкин.