Реакции в растворах

РЕАКЦИИ В РАСТВОРАХ, хим. р-ции, идущие между растворенными в-вами, а также между растворенным в-вом и р-рителем. Как правило, р-ритель принимает непосредств. участие в хим. взаимодействии. С одной стороны, р-ритель проявляет себя как сплошная среда (континуум), характеризующаяся вязкостью, диэлектрич. проницаемостью, поляризацией и т. п.; с другой стороны-как совокупность молекул, обладающих размером, дипольным моментом, поляризуемостью и участвующих в межмолекулярном взаимодействии друг с другом и с молекулами растворенного в-ва, к-рое м. б. описано соответствующими потенциалами. Молекулы р-ри-теля образуют упорядоченные структуры на расстояниях, сравнимых с межмолекулярными (ближний порядок), что отражается видом корреляц. ф-ции распределения (см. Жидкость). Сольватные оболочки, окружающие реагирующие частицы в р-ре, характеризуются координац. числом и ре-лаксац. параметрами.

Термодинамика. Если при переходе реагентов А и В из газовой фазы в р-р не происходит изменения в направлении р-ции А + В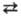С и составе продуктов, положение равновесия Р. в р. зависит от своб. энергии сольватации р-рителем 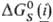исходных реагентов и продуктов. Стандартная энергия Гиббса Р. в р. 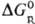связана со стандартной энергией Гиббса соответствующей газофазной р-ции 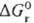соотношением: 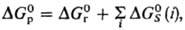где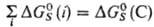

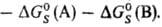
Величина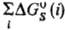м. б. очень значительной, сравнимой с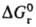 или даже превышающей ее. Напр., в случае ионов в полярных р-рителях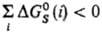и если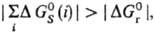в р-ре энергетически выгодными становятся процессы ионизации, к-рые в газовой фазе практически не идут.

Кинетика. Важнейшей особенностью Р. в р. является многообразие равновесных форм, в к-рых исходный реагент может участвовать в р-ции. В зависимости от природы р-рителя и реагента в р-ре может происходить, с одной стороны, ионизация молекул растворенного в-ва с образованием ионных пар (контактных и сольватно разделенных) и дальнейшей их диссоциацией на ионы, с другой - образование гомо- и гетероассоциатов и кластеров с участием молекул как реагентов, так и р-рителя. Последнее характерно для молекул, образующих водородные связи (Н-связи).

Наблюдаемые константы скорости Р. в р., за редким исключением, являются эффективными величинами. Простые порядки р-ции, полученные при обработке данных кинетич. эксперимента, проведенного в узком интервале т-р и концентраций, как правило, являются кажущимися и не отражают истинной молекулярности р-ции, то же откосится и к энергии активации р-ции. Поэтому, прежде чем обсуждать вопрос о влиянии р-рителя на константу скорости Р. в р., надо установить, какая из форм исходного реагента принимает участие в лимитирующей стадии сложной р-ции. Это же относится к квантовохим. расчетам, в основу к-рых следует закладывать строение частиц не исходных реагентов, а тех форм, в к-рых эти соед. реагируют в р-ре.

При наличии в системе разл. активных форм исходных реагентов р-ция идет по неск. каналам. Наблюдаемая константа скорости является ф-цией констант скорости р-ций в каналах и соотношений между концентрациями разл. форм. Напр., если в-во М:А, участвующее в р-ции 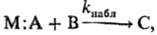образует в р-ре ионные пары и своб. ионы, в р-ции могут участвовать все формы, находящиеся в равновесии: молекулярная М:А, контактные ионные пары М ⁺ · А^- , сольватно разделенные ионные пары М⁺|S|А^-(S-p-ритель), своб. ионы М⁺+А^-; каждой из этих форм соответствует своя константа скорости k_i. Наблюдаемая константа скорости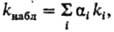где a(i)-доля i-й формы.

В случае, когда присутствуют только две формы, напр. М:А и М ⁺·А^-, реагирующие с В в двух простых параллельных стадиях с константами скорости k₁ и k₂ соотв., k_набл = ak₁+ +(1—a)k₂. Если константа равновесия перехода между двумя формами К=(1—a)/a, то вышеприведенное выражение принимает вид: k_набл=(k₁ + Kk₂)/(1+К), Обычно реакц. способность ионной пары выше, чем молекулы, и в случае, когда Kk₂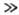k₁, выражение упрощается: k_набл= = Kk₂/(1 + К).

Для р-ции типа X+Y: продукты, где X и Y-соед., способные образовывать Н-связи: вода, спирты, амины, карбоновые к-ты и т. п., характерно участие гомоассоциатов Х_n и Y_m, а также гетероассоциатов X_pY_q. Во мн. случаях р-ции между мономерными формами X и Y практически отсутствуют. Имеют место след. равновесия:

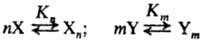
(n = 1, 2, ...,р, m= 1, 2, ..., q)

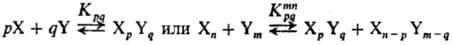
Благодаря ассоциации удлиняются хим. связи, увеличиваются эффективные электрич. заряды на атомах реагентов. Квантовохим. расчет показывает, напр., что в результате димеризации метанола связь О—Н удлиняется на 4%, заряд-на атоме Н увеличивается на 25% и на атоме О-на 14%. Дальнейшая ассоциация приводит к еще большему росту зарядов. Указанные изменения в структуре молекулы, как правило, приводят к увеличению реакц. способности спирта. Помимо этого, меняется сам механизм р-ции в связи с возможностью образования циклич. предреакц. комплексов и циклич. переходных состояний. При этом уменьшаются стерич. затруднения и снижается энергетич. барьер при осуществлении элементарного акта р-ции: разрыв и образование связей в циклич. "заготовке" происходят согласованно (см. Согласованные реакции). Напр., в р-ции ROH + + R'NCO : R'NHCOOR мономер спирта практически не-реакционноспособен и р-ция идет только с участием диме-ров и тетрамеров спирта:

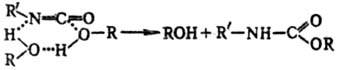
Существенно, что наряду с активными гетероассоциатами X_pY_q, оптимальными по составу и структуре ("удачными микрореакторами"), через к-рые осуществляется образование продукта (канал выхода реакции), в р-ре возникает большое число разнообразных неактивных (тупиковых) ас-социатов X_iY_j, в виде к-рых находится осн. масса реагентов ("канал накопления"). Схема Р. в р. с участием ассо-циатов выглядит след. образом:

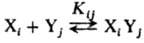(канал накопления)

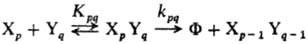(канал выхода)

Согласно схеме, при наличии одного канала выхода скорость образования продукта Ф пропорциональна концентрации реакционноспособного ассоциата [Х_рY_q]: w = = d[Ф]/dt = k_pq[Х_рY_q]; эта концентрация является ф-цией констант равновесия К_p, К_q, К_pq, К_i, K_j, К_ij и стехиометрич. коэффициентов i,j,p,q. Наблюдаемый порядок Р. в р. в этом случае зависит от соотношения стехиометрич. коэф., с к-рыми входят реагенты в каналы накопления и выхода. Энергия активации р-ции и предэкспоненц. множитель, формально найденные из аррениусовской температурной зависимости наблюдаемой константы скорости, являются сложными величинами, включающими термодинамич. характеристики равновесий образования вышеуказанных гомо- и гетероассоциатов.

Роль диффузии. В отличие от газовой фазы, реагирующие частицы в р-ре окружены молекулами р-рителя и не могут претерпевать двойных соударений. Сближение частиц А и В, необходимое для осуществления р-ции А + В : продукты, реализуется путем взаимной диффузии с относит. коэффициентом D_АВ=D_А+D_В, где D_А и D_В-коэф. диффузии А и В в р-ре. Число "первых встреч", в результате к-рых образуется "диффузионная пара"-две расположенные рядом незаряженные частицы, окруженные молекулами р-рителя ("клеткой"),-рассчитывается по ф-ле Смолуховского: Z_B = 4pD_АВ(r_А + r_B) [см³/(молекул·с)], где r_А и r_B-радиусы А и В. Для близких по размеру частиц (r_А ! r_B) Z_B = = 8 RT/3·10³h [л/(моль·с)] (T-абс. т-ра, R-газовая постоянная). Здесь Z_B-число первых встреч за 1 с при единичных концентрациях А и В, h-вязкость среды. Как видно из ур-ния, Z_B обратно пропорционально вязкости.

Если скорость р-ции между А и В очень велика (рекомбинация своб. радикалов или разнозаряженных ионов, электронные и протонные переходы), т.е. р-ция происходит уже при первой встрече, скорость ее лимитируется диффузией (см. Диффузионно-контролируемые реакции). Константа скорости такой р-ции k_диф ! Z_B и также обратно пропорциональна вязкости. В случае обычных молекулярных и ионных р-ций (энергия активации Е > 40 кДж/моль) реагенты А и В, попав в "клетку" р-рителя, претерпевают множественные соударения, число к-рых п_кл тем больше, чем дольше они там находятся, т. е. чем больше вязкость среды (п_кл ~ h). Время пребывания частицы в клетке т (среднее "время оседлой жизни", по Я. И. Френкелю) м. б. найдено по ур-нию: т=т₀exp(E_клl/RT), где т₀!10^-13-10^-12 с-период колебаний частиц в клетке, Е_кл энергия, необходимая для выхода частицы из клетки. Для воды т₀ = 1,4·10~¹² с, т= 1,7·10^-9с, E_кл!7RT, т.е. при 300 К E_кл! 17кДж/моль. Величина п_кл ! т/т₀ = ехр(E_кл/RT), что для большинства жидкостей составляет 10² — 10⁴.

Полное число соударений Z = Z_Bп_кл, т.е. равно произведению двух независимых вероятностей, одна из к-рых прямо пропорциональна, другая - обратно пропорциональна вязкости. Поэтому константа скорости обычной р-ции не зависит от вязкости р-рителя, вплоть до стеклообразного состояния.

Если собственно хим. превращение в диффузионной паре (константа скорости k_кл) происходит настолько медленно, что необходимо учитывать не только константу скорости образования пары k₁ = k_диф, но и константу скорости се распада k₂, то Р. в р. можно представить схемой:

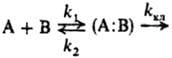продукты

Диффузионная пара (А: В) обычно является статистич. образованием ("столкновительным комплексом", по Я. Бьерру-му). Однако при наличии между А и В межмол. взаимод. пара (А:В) м.б. комплексом (напр., донорно-акцепторным) или ассоциатом, в состав к-рого могут входить и молекулы р-рителя. По сути, упоминавшиеся выше гетероассоциаты-это сложные диффузионные пары. Согласно этой схеме, Р. в р.-двустадийный процесс, в к-ром первая стадия диффузионная, а вторая - химическая, т е. бимолекулярная

Р. в р. сводится к мономолекулярному превращению диффузионной пары. В стационарном состоянии реагирующей системы наблюдаемая константа скорости в ур-нии d [продукт]/dt = k_набл [А]·[В] имеет вид: k_набл = k₁·k_кл/(k₂+k_кл). Если хим. р-ция в клетке медленнее, чем диффузия (k₂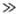k_кл), выражение для k_наб упрощается: k_набл = K_АВk_кл, где К_АВ = = k₁/k₂, по сути, есть константа равновесия образования диффузионной пары.

Теория активированного комплекса используется для расчета истинной константы скорости элементарной Р. в р. Предполагается, что точно определена форма реагента (хим. субстрат), превращение к-рого приводит к образованию продуктов, причем лимитирующей стадией является не диффузия молекул в клетку р-рителя, а собственно превращение субстрата внутри клетки (кинетич. режим протекания р-ции). Для Р. в р., к-рые протекают при постоянном давлении, осн. соотношение теории связывает константу скорости р-ции k со своб. энергией активации DG^. - изменением энергии Гиббса системы при переходе от реагентов к переходному состоянию (ПС):

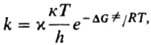
где Т-.абс. т-ра, к и h-постоянные Больцмана и Планка соотв., х - трансмиссионный множитель, к-рый в рамках теории активир. комплекса не м. б. вычислен и считается равным 1. Величину DG^. можно представить в виде суммы двух слагаемых, одно из к-рых (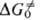) учитывает изменение своб. энергии изолир. субстрата, второе (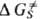)-эффекты сольватации:

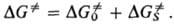
Последние особенно существенны при сильном электроста-тич. взаимод. между субстратом и средой при условии, что распределения электрич. заряда в субстрате и в ПС значительно различаются, т.е. р-ция является процессом с переносом заряда. Напр., в простейших р-циях нуклеоф. замещения S_N2:

Х^- +СН₃Y:[Х...СН₃..Y]^-:XCH₃ + Y^-

(X, Y-Hal, ОН и т.п., Х^-, Y^--соответствующие анионы), отрицат. заряд в реагентах локализован на частице X, а в ПС делокализован. ПС сольватировано слабее реагентов, т.е. 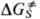положит. величина. В полярных р-рителях константа скорости р-ций типа S_N2 уменьшается на 10-20 порядков по сравнению со значением в газовой фазе. Существ. вклад в величину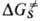могут давать также изменения прочности водородных связей субстрата и среды. Для р-ций неполярных молекул и для р-ций в неполярных апротонных р-рителях, когда электростатич. взаимод. слабы и прочные водородные связи не образуются, истинные константы скорости, как правило, мало отличаются от газофазных значений.

Для газофазных р-ций аррениусовскую энергию активации отождествляют с высотой барьера на поверхности потенциальной энергии (ППЭ), а слабо зависящий от т-ры предэкспоненц. множитель выражают через вклады реагентов и ПС в энтропию системы. Своеобразие Р. в р. состоит в том, что в ППЭ в качестве независимых переменных наряду с координатами хим. субстрата x_i (длинами связей, валентными углами и т. п.) введены координаты среды - изменения положения и ориентации молекул р-рителя относительно молекул субстрата и друг друга. При этом существует огромное кол-во конфигураций сольватной оболочки хим. субстрата, соответствующих разл. локальным минимумам ППЭ. Эти минимумы близки по энергии и разделены невысокими (несколько кДж/моль) потенц. барьерами. В такой ситуации к.-л. один определенный минимум теряет значение и рассматривают усредненное влияние всех конфигураций сольватной оболочки на энергетику хим. превращения субстрата. Усредненная таким образом ППЭ представляет собой поверхность свободной энергии (ПСЭ) G(x_i), зависящую лишь от координат хим. субстрата. Изменение своб. энергии DG^. отождествляют с высотой барьера на ПСЭ, разделяющего минимумы реагентов и продуктов. При вычислении ПСЭ учитывают взаимод. молекул р-рителя между собой и с молекулами субстрата; при сильном взаимод. ПСЭ существенно отличается от газофазной ППЭ. Сольватация меняет не только высоту барьера, но и структуру субстрата в стационарных точках (реагенты, ПС), поэтому вычисление сольватац. вклада 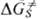не сводится к простому расчету своб. энергии сольватации для соответствующих газофазных структур.

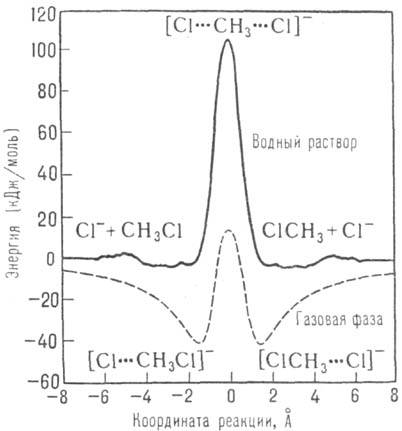
Прямое вычисление энергетич. профиля вдоль координаты р-ции на ПСЭ и последующий расчет константы скорости возможны с применением методов Монте-Карло и мол. динамики (см. Молекулярная динамика). Для упоминаемой р-ции S_N2 при X, Y = С1 в газовой фазе ППЭ, полученная квантовохим. расчетом, имеет сложный профиль с двумя ямами, соответствующими образованию пред-и послереакционного комплексов. Для той же р-ции в воде профиль ПСЭ, полученный сочетанием квантовохим. расчета с методом Монте-Карло, имеет обычный вид кривой с потенц. барьером (см. рис.). Кол-во молекул р-рителя, к-рые следует учесть при расчете ПСЭ, велико. Как минимум, это молекулы, входящие в неск. ближайших коорди-нац. сфер хим. субстрата. Для р-ции S_N2 в воде, напр., явно учитывали 250 молекул Н₂О; полученное значение DG^. = = 110 кДж/моль при 25 °С хорошо согласуется с экспериментом. Наконец, применение методов мол. динамики позволяет выйти за рамки теории активир. комплекса, рассчитав трансмиссионный множитель х в выражении для константы скорости.

Энергетич. профиль пов-сти потенц. энергии для р-ции S_N2 в газовой фазе (пунктирная линия) и пов-сти своб энергии для р-ции в р-ре (сплошная линия).

Континуальная модель растворителя. Высоту барьера ПСЭ можно определить с меньшими вычислит. затратами на основе континуальной модели р-рителя. Обычно этот подход применяют к р-циям с переносом заряда в апротонных полярных средах, когда взаимод. среды и субстрата в осн. электростатическое. Р-ритель рассматривают как сплошной диэлектрич. континуум с диэлектрич. проницаемостью e_s. В нем вырезают полость, в к-рую помещен реагирующий хим. субстрат (диэлектрич. проницаемость полости равна 1). Зарядовое распределение субстрата поляризует среду; поле наведенной поляризации среды, в свою очередь, меняет зарядовое распределение субстрата. Результирующая поляризация среды Р(r) в точке пространства вне полости вместе с результирующим зарядовым распределением субстрата r(r) рассчитывается методом итераций. На каждой итерации электростатич. расчет Р(r) комбинируют с квантовохим. вычислением r(r). Этот метод расчета электростатич. составляющей сольватации наз. методом самосогласованного реакционного поля (метод ССРП). В простейших реализациях, если моделировать хим. субстрат в виде помещенных в центр сферич. полости точечных иона и диполя, метод позволяет получить для энергии сольватации известные ф-лы Борна и Онсагера (см. Сольватация):

Динамическая континуальная модель и коллективные координаты среды. При наличии сильного взаимод. субстрата со средой необходимо в явном виде учесть зависимость ПСЭ и своб. энергии активации DG^. от изменений, происходящих в среде. Континуальная модель вводит в качестве переменных среды не элементарные смещения отдельных молекул р-рителя, а коллективные координаты (моды), описывающие согласованные комбинации большого числа элементарных смещений. Такой подход в принципе позволяет выделить одну или неск. существенных для описания р-ции коллективных координат (кинетически активных мод) и ограничиться их явным рассмотрением.

При чисто электростатич. взаимод. среды и субстрата в качестве коллективной координаты среды принимают т. наз. инерционную поляризацию P_in(r), т.е. часть полной поляризации среды, из к-рой исключена поляризация электронных оболочек молекул р-рителя (С. И. Пекар, 1951; Р. Маркус, 1956). Инерционная поляризация изменяется со временем независимо в каждой точке r трехмерного пространства, т.е. ее значения в каждой точке-независимые динамич. переменные. Запись P_in(r) означает, что рассматривается бесконечный набор (континуум) всех таких переменных. При заданном зарядовом распределении субстрата r_а(r) ПСЭ представляет собой бесконечномерный параболоид в пространстве поляризаций. Его минимум соответствует поляризации 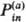(r), равновесно подстроенной под заряд r_а(r). При др. зарядовом распределении r_b(r) минимум параболоида ПСЭ смещается в др. 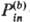точку пространства поляризации(r). Если в ходе р-ции распределение заряда субстрата меняется от r_а(r) до r_b(r), ПСЭ комбинируется из двух пересекающихся параболоидов. Такая ПСЭ описывает реорганизацию полярного р-рителя при учете одних лишь электростатич. сил.

Переходное состояние для р-ции переноса электрона характеризуется высотой барьера DG^., к-рая выражается уравнением Маркуса:

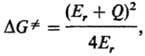
где Q-разность своб. энергий системы продуктов и системы реагентов, т.е. разность между :положениями минимумов соответствующих параболоидов на энергетич. шкале (для экзотермич. р-ций Q < О), а Е_r-т. наз. энергия реорганизации р-рителя. Этот важный параметр теории характеризует степень изменения ПСЭ при изменении распределения заряда на субстрате от r_а(r) до r_b(r). Скорость изменения поляризации среды, подстраивающейся под зарядовое распределение субстрата, к-рое меняется в ходе р-ции, определяется диэлектрич. релаксацией р-рителя. Время продольной диэлектрич. релаксации т_L является динамич. характеристикой среды, оно м. б. определено экспериментально на основе ф-лы Дебая (см. Диэлектрики).

Стохастическая теория. В динамич. теории подлежит рассмотрению огромное кол-во координат среды. Эффективный способ обойти эту трудность-рассматривать в явном виде только координаты хим. субстрата, к-рые, однако, взаимодействуют (обмениваются энергией) с неучтенными в явном виде переменными среды, т.е. образуют термодинамически открытую систему. Динамика открытых систем описывается стохастич. ур-ниями, простейшее из к-рых-уравнение Ланжевена:

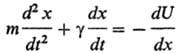+ случайная сила,

где x-динамич. переменная (обобщенная координата), m-связанная с ней масса. Первыми в правой и левой частях этого ур-ния стоят обычные ньютоновские члены: кинематич. член, пропорциональный ускорению, и регулярная сила [U(x)-потенц. энергия]. Второй член в левой части-сила трения, к-рая пропорциональна скорости dx/dt (g-коэф. трения); она описывает диссипацию энергии вследствие взаимод. координаты х со средой. Второй член в правой части-случайная сила-описывает нерегулярное воздействие среды на переменную х (при моделировании Р. в р. она обусловливает термич. активацию субстрата, необходимую для преодоления потенц. барьера). Сила трения и случайная сила связаны таким образом, что их комбинир. воздействие обеспечивает установление в системе больцмановского распределения спустя время, превышающее период релаксации переменной х.

Впервые ур-ние Ланжевена было предложено для объяснения броуновского движения взвешенных в жидкости коллоидных (т.е. макроскопич.) частиц. В теории Р. в р. координата х обычно соответствует одной из степеней свободы хим. субстрата, т.е. является микроскопич. переменной. Поэтому интерпретация коэф. у как макроскопич. трения, обусловленного вязкостью среды, неправомерна, хотя ее иногда и используют (см. ниже). Величину у следует рассматривать как феноменология, характеристику взаимод. между субстратом и средой, ее микроскопич. интерпретация требует спец. теории.

Если U(х)-потенц. кривая с барьером, ур-ние Ланжевена описывает динамику перехода системы через барьер и м. б. использовано для описания кинетики Р. в р. Приближенная теория, разработанная Г. Крамерсом (1940), дает для константы скорости k аррениусовскую зависимость от т-ры, причем энергия активации Е совпадает с высотой барьера, а предэкспоненц. множитель зависит от g. При больших g эта зависимость обратно пропорциональна. Иногда полагают, что у пропорциональна гидростатич. вязкости среды h; в таком случае расчет предсказывает зависимость k ~ 1/h) (предельный случай большой вязкости). Эксперим. данные в отдельных случаях подтверждают этот вывод. Следует помнить, что речь идет о влиянии вязкости среды на элементарный акт хим. р-ции, а не о тривиальном влиянии, к-рое всегда наблюдается, если р-ция протекает в диффузионном режиме, как было рассмотрено в соответствующем разделе данной статьи.

Перенос электрона. Для мн. р-ций, в к-рых донор электрона Д и акцептор А представляют собой комплексы переходных металлов, орг. субстраты или фрагменты биол. молекул, перенос электрона предполагается внешнесферным. Это означает, что на лимитирующей стадии р-ции внутр. координаты субстрата не меняются. Меняется только инерционная поляризация среды P_in(r) в соответствии с изменением зарядового распределения r(r). Перенос электрона м.б. адиабатическим и неадиабатическим. В первом случае рассматривается лишь изменение в ходе р-ции единственного электронного состояния (основного или возбужденного), взаимодействующей пары ДА, во втором-по крайней мере двух состояний. В случае адиабатич. переноса электрона можно пользоваться ур-нием Ланжевена, причем переменная х выражается через P_in(r), т. е. оказывается коллективной модой среды, описывающей ее реорганизацию, а коэф. трения у пропорционален времени продольной релаксации т_L, т.е. предэкспоненц. множитель А ~ 1/т_L. Такая зависимость экспериментально наблюдается для нек-рых р-ций (см. Реакционная способность). Иногда имеет место более слабая зависимость А ~ (1/т_L)^b, где b < 1, к-рую интерпретируют усложнением модели р-ции и соответствующего стохастич. ур-ния. Динамика неадиабатич. переноса электрона впервые изучалась В. Г. Левичем и Р. Р. Догонадзе (1959). В их теории Р. в р. рассматривается как безызлучат. квантовый переход, причем зависимость константы скорости от релаксац. характеристик р-рителя отсутствует.

Неравновесная сольватация. Говоря о неравновесной сольватации, обычно имеют в виду, что координата р-ции х описывает движение ядер в субстрате (а не в среде, как при переносе электрона), и в ходе элементарного акта р-ции координаты р-рителя q_v не успевают подстраиваться под движение системы по х, к-рое считается более быстрым. В предельно неравновесном случае конфигурация сольват-ной оболочки субстрата в ПС остается такой же, какой она была в конфигурации реагентов (предельный случай "замороженной" среды).

Неравновесные кинетич. режимы Р. в р. возникают, когда сильно различаются характеристич. времена, связанные с движениями в хим. подсистеме (т_x) и в среде (т_q). Из сказанного выше очевидно, что т_q следует относить именно к коллективным модам среды, а не к движениям отдельных молекул. Напр., для р-ции нуклеоф. замещения в качестве х можно выбрать антисимметричное колебание в ПС, а в качестве q - коллективную моду, зависящую от инерционной поляризации. В случае р-ций с переносом заряда подходящей оценкой для т_q является время продольной релаксации т_L; для типичных р-рителей при комнатной т-ре оно равно 10^-11-10^-12 с. Величину т_x обычно оценивают как 10^-12 с.

Динамика реагирующей системы и определяемая ею кинетика р-ции задаются системой стохастич. ур-ний для х и q. При т_q >> т_x устанавливается неравновесный кинетич. режим, при к-ром температурная зависимость константы скорости не является аррениусовской. При т_x!т_q кинетика р-ции практически равновесна, а константа скорости имеет обычный вид с аррениусовским температурным множителем.

Принципиально интересны системы, для к-рых отнощение т_q / т_x очень велико; такой кинетич. режим экспериментально обнаружен для р-ций в чрезвычайно вязких средах. Его нельзя описать с помощью константы скорости, т. к. температурная зависимость не описывается одной экспонентой. Описание таких Р. в р. возможно на основе стохастич. ур-ний с неск. переменными.

Лит.: Энтелис С. Г., Тигер Р. П., Кинетика реакций в жидкой фазе, М., 1973; Мелвин-Хьюз Е. А., Равновесие и кинетика.реакций в растворах, пер. с англ., М., 1975; Эткинс П., в кн.: Физическая химия, пер. с англ., т. 2, М., 1980, с. 439-78; Базилевский М. В., Фаустов В. И., "Успехи химии", 1992, т. 61, в. 7, с. 1185; Chandler D., Introduction to modern statistical mechanics, Oxf., 1987. С.Г. Энтелис, М.В. Базилевский.