Поляризуемость

ПОЛЯРИЗУЕМОСТЬ атомов, ионоз, молекул, способность этих частиц приобретать дипольный момент ц в электрич. поле. Появление m обусловлено смещением электронов (электронная П.) и атомных ядер (атомная П.) под действием поля; такой наведенный (индуцированный) дипольный момент исчезает при выключении поля. У полярных молекул, обладающих постоянным дипольным моментом в отсутствие поля, наведенный дипольный момент векторно складывается с постоянным.

В относительно слабых полях напряженности Е зависимость m от Е линейна; векторы m и Е связывает тензор b, являющийся количеств. мерой П. и наз. тензором П. В трехосной системе координат х, у, z

'

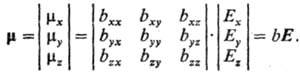
Компонента тензора b_ij представляет собой величину ди-польного момента, возникающего вдоль оси i при действии электрич. поля вдоль оси j, причем b_ij = b_ji. Тензор П. может быть представлен эллипсоидом с полуосями b₁, b₂, b₃, равными диагональным компонентам, в такой системе координат, когда все недиагональные компоненты b_ij (i.j)равны нулю.

На практике обычно пользуются двумя инвариантами тензора П.: средней П. b = (b₁ + b₂ + b₃)/3 и молекулярной анизотропией П. g² = [(b₁ — b₂)² + (b₂ — b₃)² + (b₃ — — b₁)²]/2. Если b₁ = b₂ = b₃, частица наз. изотропно поляризуемой. При наличии у молекулы оси симметрии третьего порядка (или более высокого) b₂ = b₃ и анизотропия П. g = b₁ — b₃, причем она принимается положительной для вытянутых эллипсоидов П. и отрицательной для сплюснутых. Величины b и у имеют размерность объема, порядок-10^-30м³; в СИ учитывается электрич. постоянная e₀ (ди-электрич. проницаемость вакуума) и П. имеет размерность Кл·м²/В, или Ф·м², а порядок величины-10^-41 Ф·м².

В сильных электрич. полях зависимость m от Е перестает быть линейной. Тензорные величины, обусловливающие вклады, пропорциональные высшим степеням Е, наз. гипер-поляризуемостями первого, второго и т. д. порядков. Ста-тич. полю отвечает статическая П. В переменном поле, изменяющемся по гармонич. закону, П. зависит от его частоты со и наз. динамической П. Согласно классич. теории, для системы частиц с массами m_k, зарядами e_k и частотами собств. колебаний w_k динамическая П. равна (в СИ):

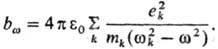
Согласно квантовой теории, молекула в поле меняет свое состояние. Если это изменение мало, возмущений теория дает след. выражение для динамической П.:

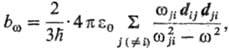
где Н - постоянная Планка, 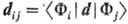- недиагональный матричный элемент оператора дипольного момента, Ф_i и Ф_j-волновые ф-ции молекулы, E_i и E_j-энергии молекулы в состояниях i и j, а w_ji = (E_j — E_i)/ђ. При w = 0 это выражение переходит в выражение для статической П.:

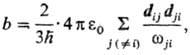
При включении электрич. поля дипольный момент m появляется не мгновенно, время т его установления зависит от природы частиц и окружающей среды. При достаточно низких w и малых т дипольный момент частиц устанавливается синфазно с изменением Е и динамическая П. практически совпадает со статической П.

П. нейтральных атомов больше, чем соответствующих катионов, и меньше, чем анионов. Для молекул вклады в П. от электронных и колебат. состояний представляют соотв. электронную и атомную П.; атомная П. составляет ок. 10% электронной П. Средняя электронная П. в постоянном внеш. поле пропорциональна рефракции молярной. Мол. анизотропия П. g² проявляется в Керра эффекте и рэлеевском рассеянии света: коэф. деполяризации света А, определяемый как отношение интенсивностей перпендикулярно и параллельно поляризованных лучей при наблюдении света в плоскости, перпендикулярной направлению распространения падающего луча, равен:

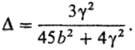
Главные полуоси b₁, b₂ и b₃ эллипсоидов П. вычисляются при наличии осевой симметрии молекулы (напр., при b₂ = = b₃) из значений средней П. и мол. анизотропии, получаемых при эксперим. изучении эффекта Керра или рассеяния света. Если все три полуоси различны, для их определения требуется привлечение неск. методов; так, если молекула обладает постоянным дипольным моментом m₀, к-рый совпадает по направлению с осью b₁, константа Керра К = =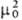(2b₁-b₂-b₃). 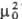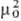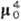Тогда b_l=(b+K/)/3, b₂ и b₃= = b-К/6b (12g² - К²/)^1/2/6. Отношение b₂ и b₃ находят на основании дополнит. данных.

Эллипсоиды П., в т.ч. для индивидуальных атомов, м.б. определены из квадратичного Штарка эффекта. Главные полуоси обычно меняются от 10^-3 до 10^-1 нм³; так, для Н₂ b₁=0,99·10^-3, b₂ = b₃ = 0,69·10^-3нм³; для бензола b₁=7,36·10^-3, b₂=b₃=11,2·10^-3 нм³; для трис-(п-хлорфенил)фосфиноксида b₁ = 36,25·10^-3, b₂=b₃=41,71x x 10^-3 нм³.

П. частиц в существ. мере определяет диэлектрич. св-ва в-ва. В частности, для в-в, состоящих из полярных молекул, связь между П. и диэлектрич. проницаемостью описывается ф-лой Ланжевена-Дебая (см. Диэлектрики). Тензорный характер П. проявляется в появлении двойного лучепреломления изотропной среды при воздействии на нее мощного светового импульса, в двойном лучепреломлении в потоке (эффект Максвелла), в магн. поле (эффект Коттона-Мутона), в явлении фотоупругости и мн. оптич. св-вах твердых и жидких тел; в ряде случаев П. может быть определена на основании этих св-в.

П. химических связей. Как правило, П. молекулы считается аддитивной по хим. связям (средняя П.-также и по атомам). При аддитивном подходе каждой связи приписывается эллипсоид П. с главными полуосями вдоль связи (продольная П. b_L) и в двух поперечных взаимно перпендикулярных направлениях; мол. эллипсоид П. получается как тензорная сумма связевых эллипсоидов П. с учетом расположения их осей. Если связь между частицами А и В имеет осевую симметрию, две поперечные П. b_T равны между собой, анизотропия П. g(А—B) = b_L(A—В)-b_T(А—В). В случае двойной связи b_T лежит в ее плоскости, а перпендикулярная этой плоскости составляющая П. наз. вертикальной П. (обозначается b_V). Такая связь описывается двумя параметрами анизотропии П.: g' = b_L — b_T, g: = b_L — b_V.

Аддитивное по связям разложение мол. эллипсоида П. обычно дает не отдельные компоненты связевых эллипсоидов П., а лишь независимые линейные комбинации этих компонентов. Так, для молекул углеводородов и их производных анизотропии П. связей С—X [обозначение S(C—X)] равны g(С—X) - g(С-Н), связей С—С [обозначение Г(С—С)] равны g(С—С)—2g(С—Н). При нек-рых дополнит. предположениях независимое определение анизотропии П. связей возможно из интенсивностей линий в спектрах комбинац. рассеяния, к-рые пропорциональны производным средней П. и анизотропии по нормальной координате; таким образом получена для связи С_sp3—Н величина g = b0,312·10^-3 нм³. При обычном аддитивном рассмотрении используют величины S(C—X). В ряде случаев удобно рассматривать тензоры групп атомов. Параметры П. связей коррелируют с их длинами и с частотами колебаний, соотносимыми этим связям. Нек-рые данные по поляризуемостям связей приведены в таблице.

Данные о П. молекул используются для изучения их строения. Стереохим. приложения основаны на сравнении экспериментально определяемых эллипсоидов П. или, чаще, непосредственно измеряемых констант Керра и мол. анизотропии П. со значениями, вычисленными по тензорной аддитивной схеме для разл. пространств. взаимных положений анизотропных фрагментов в конформерах.

Анизотропии П. связей зависят от их взаимного расположения. Сопряжения связей повышают среднюю П. (эффект иногда наз. экзальтацией П.) и влияют на мол. анизотропию П., в результате чего главные полуоси эллипсоида П. не совпадают со значениями, вычисленными в аддитивном приближении. Так, отклонения от аддитивных значений главных полуосей 1-нитро-4-хлорбензола составляют 0,74·10^-3нм³ в направлении 1-4, 0,30·10^-3нм поперек этого направления в плоскости ароматич. системы и перпендикулярно этой плоскости —0,35·10^-3 нм³. Межмол. взаимодействия приводят к появлению эффективной анизотропии П. "ван-дер-ваальсовых" молекул и к отклонениям от аддитивности таких связанных с П. св-в, как молярная рефракция, константы Керра, мол. анизотропии и др., особенно при образовании комплексов, в т.ч. с водородной связью и донорно-акцепторных.

П. играет определяющую роль в оптич. активности и нек-рых др. оптич. св-вах в-в. Она является осн. понятием в теории дальнодействующих сил притяжения (дисперсионных и индукционных) между нейтральными атомами и молекулами (см. Дисперсионное взаимодействие).

П. определяет величины дипольных моментов, индуцируемых на связях внутримол. электрич. полями, к-рые создаются совокупностью зарядов молекулы. Во мн. случаях влияние заместителей на хим. и физ. св-ва молекул также обусловлены прежде всего П. В частности, вклад DЕ в изменение энергии молекулы при введении заместителя определяется взаимод. заряда или дипольного момента, связанного с реакц. центром, с дипольным моментом, индуцируемым заместителем (см. Индуктивный эффект). Наиб. существенны эти вклады для малополярных углеводородных заместителей. Так, поляризационное взаимод. обеспечивает более 80% изменения рК_а при переходе от уксусной к-ты к пропионовой. Проявление эффектов, связанных с П. заместителей, особенно алкильных радикалов, отмечено в закономерностях изменения констант скорости и констант равновесия хим. р-ций, физ. св-в в-в.

Лит.; Верещагин А. Н., Поляризуемость молекул, М., 1980; его же, Характеристики анизотропии поляризуемости молекул, М., 1982; Келих С., Молекулярная нелинейная оптика, пер. с польск., М., 1981; Le Fevre R.J.W., "Adv. Phys. Org. Chem.", 1965, v. 3, p. 1-90. А. Н. Верещагин.