Политонные перегруппировки

ПОЛИТОННЫЕ ПЕРЕГРУППИРОВКИ (политональные перегруппировки) (от греч. polys - многочисленный и topos-место), взаимные превращения между разл. изомерами, ML_x, имеющими строение координационных полиэдров или многоугольников-т. наз. политопных изомеров, или политопов. Понятие о политопах в общем случае не связано с их реальным временем жизни.

П. п. протекают в результате изменения углов политопа (изгибание) или длин его ребер (растяжение-сжатие; см. также Псевдовращение). Грани политопа - равносторонние треугольники и(или) квадраты. Как правило, политоп, содержащий только треугольные грани, является основным (энергетически предпочтительным), все другие - альтернативными. Осн. политоп для х = 4 - правильный тетраэдр, х = 5 -тригон. бипирамида, х = 6 -правильный октаэдр и т.д. Альтернативные политопы: х =4-квадрат, х = 5-квадратная пирамида (1 квадратная грань), х = 8-квадратная антипризма (2 квадратные грани) и т.д. В стерео-химически нежестких системах (см. Нежесткие молекулы)основные и альтернативные политопы энергетически близки друг другу. На рис. представлены нек-рые случаи П. п. соед. ML_х (стрелками показаны способы движения лиган-дов).

Для описания механизмов П. п. используют теорию групп. Применяют два независимых способа: квантовохим. расчеты и метод Мьюттертиза, основанный на анализе совокупности структурных данных о внутримолекулярных искажениях в однотипных системах (эти искажения отождествляют с механизмом П. п.).

Экспериментально наиб. изучены П. п. для систем с х = 3-5. При х — 3 происходит П. п. пирамида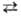плоская форма (см. Пирамидальная инверсия). В тетракоординац. системах, когда М - непереходный элемент, вероятность П. п. крайне низка вследствие высокой устойчивости тетраэдрич. формы (время жизни тетраэдрич. молекулы СН₄ оценивается в 10¹⁵ с).

В то же время с высокой скоростью протекают П. п. в тех системах, где М-переходный элемент, напр. в тетракоординац. комплексах Ni²⁺, Pt²⁺ (квадрат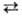тетраэдр). Широко представлены П. п. в пентакоординац. системах, для к-рых разность энергий тригон. бипирамиды (D_3h)и квадратной пирамиды (С_4u) обычно весьма мала (~25,14 кДж/моль для C1₂PF₃ и Br₂PF₃).

Обязат. условие реализации П. п.-соответствие основного политопа минимуму потенц. энергии. Если интермедиаты в к.-л. р-ции содержат в качестве центр. атома элементы 3-го и высших периодов, их структуры являются в осн. производными от структуры тригон. бипирамиды и способны к низкобарьерным П. п. В этих случаях стадия П. п. интер-медиатов имеет особое значение для характеристики стерео-хим. курса р-ций. Напр., экспериментально доказанное сохранение стереохим. конфигурации атома Р в результате перегруппировки является следствием включения как промежут. стадии П. п.:сохранение стереохим. конфигурации атома Р в результате перегруппировки является следствием включения как промежут. стадии П. п.:

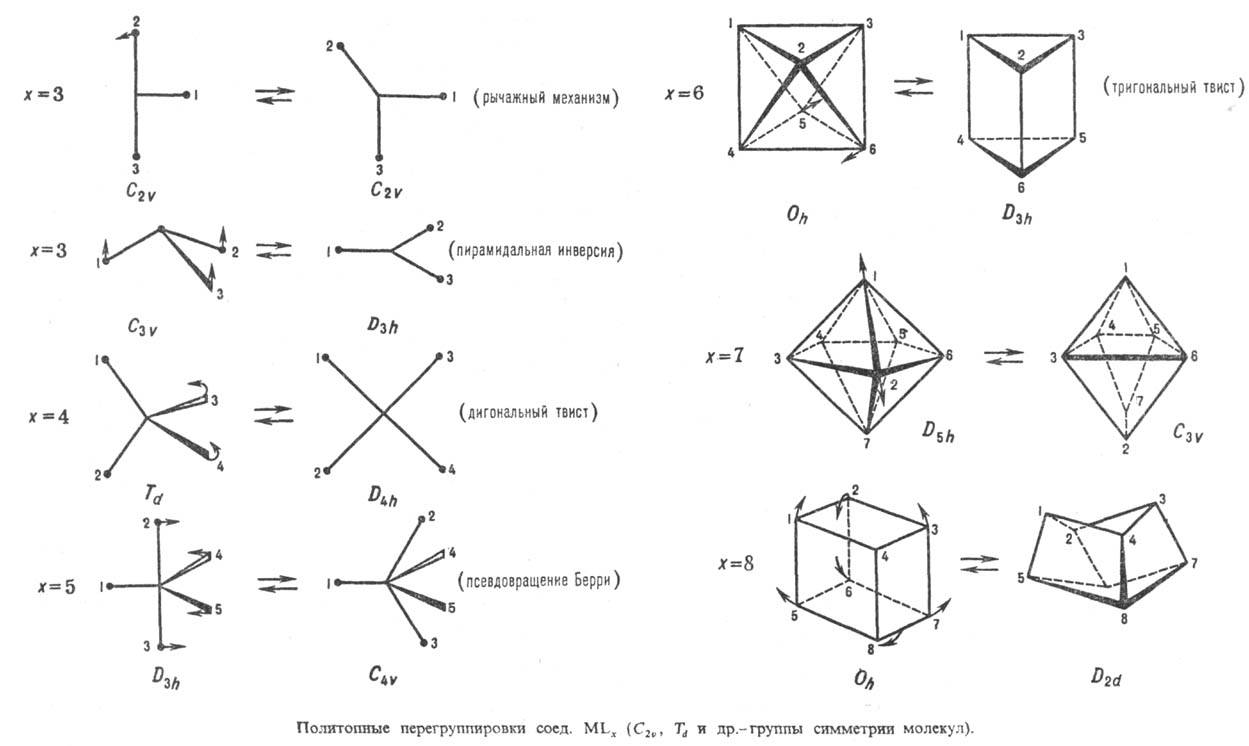
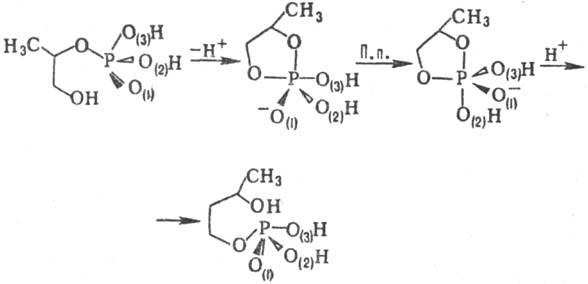
Понятие П. п. ввел Э. Мьюттертиз в 1969.

Лит.: Минкин В. И., Симкин Б. Я., Миняев Р. М., Квантовая химия органических соединений. Механизмы реакций, М., 1986; Muetterties E.I., "Асе. Chem. Res.", 1970, v. 3, №7, p. 266-73; Muetterties E. L., Guggen-berfcer L. J., "J. Amer. Chem.Soc.", 1974, v. 96, № 6, p. 1748-56.

M. E. Клецкий.