Переноса процессы

ПЕРЕНОСА ПРОЦЕССЫ, необратимые процессы пространств. переноса массы, импульса, энергии или др. Причины этих процессов-пространств.неоднородности состава, скорости движения частиц системы, т-ры. Перенос происходит в направлении, обратном градиенту концентрации, т-ры или др., что приближает систему к равновесию.

П. п. в покоящейся среде осуществляются только в результате хаотич. движения молекул (мол. перенос). В текущих средах к этому механизму переноса добавляется конвектив-ный перенос, а при высоких числах Рейнольдса еще и турбулентный перенос, связанный с хаотич. перемещением вихрей. Общую феноменологич. теорию П. п., применимую к газообразной, жидкой или твердой системе, дает термодинамика необратимых процессов.

П. п. при турбулентном режиме движения жидкости в пространстве с учетом молекулярного, конвективного и турбулентного механизмов переноса описывают с помощью выражений (1)-(3) для вектора плотности потока массы j_А, тензора плотности потока импульса несжимаемой ньютоновской жидкости П_ik [жидкость считается несжимаемой, если число Маха не превышает величину 0,14; в противном случае необходимы поправки., приводящие к появлению дополнит. членов в ур-нии (2)] и вектора плотности потока теплоты :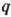

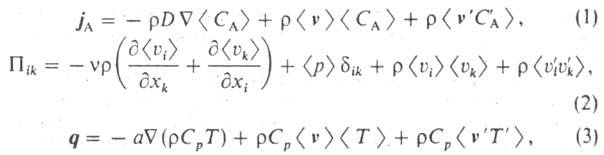
где 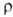плотн. жидкости; С_А, v, T -мгновенные значения соотв. концентрации компонента А в смеси, вектора скорости и т-ры; С'_А, v', T' их пульсац. составляющие; 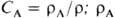-объемная массовая концентрация компонента А; 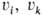-компоненты мгновенного значения скорости в прямоугольных декартовых координатах; 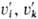-компоненты пульсац. значений скорости; D, v и a-коэффициенты соотв. мол. диффузии, кинематич. 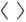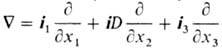вязкости и температуропроводности; p мгновенное значение давления; С_р теплоемкость при постоянном давлении; x_i,·, x_k-координаты прямоугольной декартовой системы координат; i, k = 1, 2, 3-индексы координат и компонент скорости; -оператор осреднения переменных величин по времени в рассматриваемой точке пространства; -оператор набла; i₁, i₂, i₃ -направляющие орты прямоугольной декартовой системы координат (единичные векторы); дельта-символ Кронекера.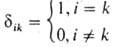

Составляющие плотностей потоков массы, импульса и теплоты в ур-ниях (1)-(3) описываются выражениями (4)-при молекулярном, (5)-при конвективном и (6)-при турбулентном механизмах переноса:

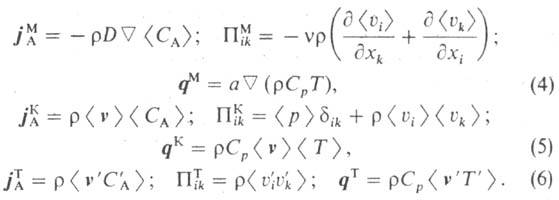
При ламинарном режиме течения: C'_A = v' = T' = 0 и в приведенных выше ур-ниях осредненные по времени значения переменных приобретают смысл мгновенных величин; поэтому в ур-ниях (1)-(3) следует принять = С_А, = v, 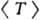— T и опустить составляющие (6).

В покоящейся среде конвективный механизм переноса отсутствует, поэтому при постоянном значении r получают ур-ния, дающие трехмерную формулировку закона Фика и ур-ния Фурье:

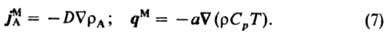
Из ур-ний (7) видно, что перенос массы (диффузия) происходит при наличии в системе градиента концентрации, а перенос теплоты (теплопроводность) - вследствие градиента т-ры. Строго говоря, движущей силой диффузии является градиент хим. потенциала, к-рый лишь вблизи положения равновесия приводится к градиенту концентрации, фигурирующему в ур-нии закона Фика. Однако практич. необходимость выражать диффузионный поток через градиент хим. потенциала (что существенно усложняет задачу) возникает лишь в спец. случаях, напр. при расчете процесса вблизи критич. точки. Законы Фика и Фурье не учитывают взаимное влияние потоков при переносе массы и теплоты (перекрестные процессы).

При существ. градиентах т-ры и давления (последнее м. б. вызвано, напр., внеш. полем) необходим учет дополнит. потока массы вследствие градиентов т-ры (термодиффузия) и градиентов давления (бародиффузия), а также учет дополнит. потока теплоты, вызванного переносом массы. При определенных условиях для перекрестных потоков выполняется теорема Онсагера.

Составляющая тензора 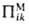в ур-нии (4), для к-рой при ламинарном режиме течения принимают 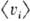=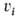, 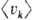= 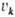, получила назв. вязкого тензора напряжений.

Особенно простой вид принимают ур-ния (4) для одномерных систем. Напр., плотность мол. потока импульса при течении с градиентом скорости u_x = f(y), u _y = u_z = 0 выражают в виде закона вязкого течения Ньютона:

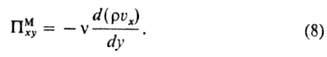
Аналогичные соотношения имеют место для плотностей одномерных потоков массы и теплоты. В случаях двух- и трехмерных потоков 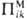представляет собой тензор с девятью компонентами, а 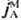, 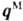-векторы с тремя компонентами.

Для неньютоновских жидкостей перенос импульса нельзя описать в виде простого градиентного закона (8). Соотношение между плотностью вязкого потока импульса и градиентом скорости для неньютоновских жидкостей определяют по моделям Шведова-Бингама, Оствальда - Вейля, Эйринга и др.

В настоящее время турбулентные потоки [ур-ние (6)] не м. б. определены теоретич. путем. Согласно гипотезе Буссинеска, между вязким и турбулентным потоками импульса имеется аналогия:

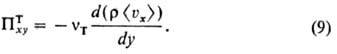
Величину v_т обычно наз. турбулентным коэф. кинематич. вязкости, или вихревой вязкостью. Существуют и др. способы (приближенные) выражения связи плотности турбулентного потока импульса с осредненными характеристиками течения-теория пути перемешивания Прандтля, гипотеза подобия Кармана и др.

Гипотезу Буссинеска используют также при описании процессов турбулентного переноса массы и теплоты; напр., плотность турбулентного потока массы по оси x выражают ур-нием:

Ур-ния (9) и (10) являются, по существу, определениями коэф. турбулентной диффузии D_ти вязкости. Трудность описания П. п. с помощью коэф. D_T, v_т и температуропроводности a_тзаключается не только в их сложной зависимости от характеристик турбулентного потока, но и в том, что турбулентные потоки не всегда пропорциональны соответствующим градиентам. Достоинством же данного приближенного подхода является непосредств. учет осн. особенности турбулентных течений-аналогии между процессами турбулентного переноса массы, импульса и теплоты, что проявляется в приближенном равенстве D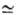_тv_т = a_т.

Турбулентный перенос вдали от пов-стей, ограничивающих область течения, во много раз превышает молекулярный. Так, напр., у газов D ~ 10^-5 м²/с, а значения D_T при течении в трубах находятся в пределах от 10^-4 до 10^-2 м²/с. Значение отношения D/D_T остается небольшим и при течении жидкостей ~10^-6-10^-4.

Гипотезу, согласно к-рой перенос определяется градиентом параметра в рассматриваемой точке пространства в данный момент времени, используют для самых разл. процессов, напр. при описании диффузии в пористых материалах, продольного перемешивания в каналах, заполненных насадкой или зернистым слоем, и т.д. Из этой гипотезы, в частности, следует, что локальные концентрац. возмущения проявляются мгновенно во всех точках системы. Но скорость распространения концентрац. возмущений не м. б. больше средней скорости молекул. Учет конечной скорости переноса массы, импульса или теплоты приводит к релак-сац. ур-ниям. В простейшем случае одномерной диффузии в отсутствие хим. превращений связь между плотностью диффузионного потока и градиентом концентрации в системе координат, неподвижной относительно среды, имеет вид:

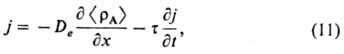
где D_е-коэф. эффективной диффузии (при рассмотрении молекулярных П. п. D_е следует заменить на коэф. D); т-время релаксации диффузионного процесса, характеризующее "память среды"; t- время. По порядку величины т совпадает со временем своб. пробега диффундирующих частиц. Аналогичные ур-ния м. б. записаны для плотности потока импульса и теплоты.

Необходимым (но недостаточным) условием применимости законов Фика, Фурье и Ньютона является незначительность изменения соответствующей концентрации за время т или на расстояниях, проходимых движущейся жидкостью за время т. Для мол. процессов время релаксации чрезвычайно мало (~ 10^-10 с), чем, в частности, оправдывается применимость простых градиентных законов. При этом физически несостоятельное допущение о бесконечной скорости распространения возмущений не играет большой роли, т. к. область заметного влияния концентрац. возмущений оказывается ограниченной и распределение концентрации внутри этой области м. б. удовлетворительно описано на основе ур-ний (7) и (8).

Обобщение законов переноса с учетом релаксац. явлений необходимо, напр., для массопереноса в капиллярнопорис-тых телах, турбулентной диффузии при малых временах рассеяния частиц примеси, при наличии быстрых хим. превращений. Особое значение имеет учет релаксац. эффектов при описании продольного перемешивания в хим. аппаратах, обусловленного гидродинамич. неоднородностями разл. масштаба.

Дифференц. ур-ния конвективной диффузии, движения жидкости (ур-ние Навье Стокса) и переноса тепла получают с помощью выражений (1)-(3) на основании законов сохранения массы и энергии:

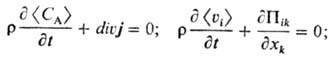
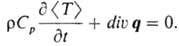
Получающиеся при этом дифференц. ур-ния, дополненные ур-нием неразрывности и соответствующими начальными и граничными условиями, позволяют определять концентрац.. скоростные и температурные поля в гомог. системах. П. п. в гетерог системах рассматривают в механике многофазных сред. О П. п. в электрич. поле см. Электроперенос.

Лит. Grоот С Мазур П Неравновесная термодинамика, пер с англ. , M 1964. Толубинский E В Теория процессов переноса. К., 1969; Лыков А.В. Тепломассообмен. Справочник, M., 1972, Берд P Стьюарт В , Лайтфут E Явления переноса, пер. с англ., M., 1974; Ландау Л Д , Лифшиц E. M. Теоретическая физика, т. 6. Гидродинамика. 4 изд.. M., 1988

В . В. Дильман