Паули принцип

ПАУЛИ ПРИНЦИП, фундаментальный принцип квантовой механику согласно к-рому у системы тождественных элементарных частиц с полуцелым спином (фер-мионов) каждое квантовое состояние м. б. заполнено не более чем одной частицей. В. Паули сформулировал этот принцип, названный им принципом запрета, в январе 1925, незадолго до того, как была создана квантовая механика (1925-26), для объяснения наблюдаемых закономерностей в электронных спектрах атомов, помещенных в магн. поле. Согласно этой формулировке, в атоме не может существовать двух или более электронов, для к-рых значения всех четырех квантовых чисел n, l, m_i, и m_s одинаковы (см. Атом). В то время понятие спина еще не было введено, поэтому четвертое квантовое число не описывалось В. Паули никакой моделью. Он назвал связанное с ним св-во "характерной двузначностью квантовых свойств электрона, которую нельзя описать классически".

Впоследствии было показано (П. Дирак, 1926), что П. п. является следствием антисимметричности волновой ф-ции системы относительно перестановок электронов. В случае системы из N невзаимодействующих электронов антисимметричная волновая ф-ция Y(x₁, x₂, ..., x_N) м. б. представлена в виде определителя (детерминанта), составленного из волновых ф-ций электронов y_kp (x_i) в квантовых состояниях k_p , характеризуемых каждое четырьмя квантовыми числами (x_i - совокупность пространств. координат и спина i-го электрона):

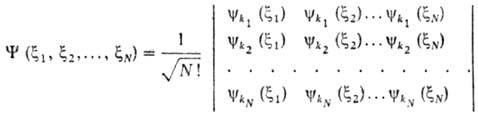
Если к.-л. две строки детерминанта совпадают, он тождественно обращается в нуль. Отсюда следует, что все наборы квантовых чисел k_p должны быть разными, т. е. не м. б. двух электронов в одном состоянии.

В дальнейшем принцип запрета был сформулирован для всех известных частиц, а не только для электронов (В. Паули, 1940). А именно: в системе тождеств. частиц со спином s осуществляются только такие состояния, для к-рых полная волновая ф-ция при перестановке любой пары частиц умножается на (—1)^2s, т.е. волновая ф-ция симметрична для целочисленных s (система частиц подчиняется статистике Бозе-Эйнштейна) и антисимметрична при полуцелых s (статистика Ферми-Дирака). Частицы с целыми значениями спина наз. бозонами, с полуцелыми - фер-мионами.

Принцип запрета относится и к перестановочной симметрии составных частиц, напр, атомных ядер. В зависимости от спина ядра можно говорить о ядрах-бозонах и ядрах-фермионах. Учет П. п. для ядер молекулы проявляется, в частности, во вращательных спектрах. Напр., в молекуле ¹⁶O₂ ядра атомов ¹⁶O состоят из четного числа нуклонов-фсрмионов и потому имеют целочисл. спин (являются бозонами). Это означает, что волновая ф-ция молекулы ¹⁶O₂ должна быть симметричной относительно перестановок ядер. Это приводит к запрету всех вращат. уровней энергии с нечетными значениями вращат. момента, что подтверждается наблюдаемыми закономерностями во вращат. спектрах.

Понятие квантового состояния частицы в системе справедливо в тех случаях, когда взаимод. между частицами можно заменить нек-рым эффективным полем, а каждую частицу можно характеризовать индивидуальным набором квантовых чисел; при строгом рассмотрении системы взаимод. частиц существуют только квантовые состояния всей системы в целом. Одночастичное приближение лежит в основе метода самосогласов. поля (метод Хартри-Фока; см. Молекулярных орбиталей методы), широко применяемого в теории атомных и мол. спектров, квантовой теории хим. связи, при описании оболочечных моделей атома и ядра и т.д.

П. п. в рамках одночастичного приближения позволяет обосновать периодич. систему хим. элементов Д. И. Менделеева, т.к. наличие в одном состоянии только одного электрона объясняет последовательность заполнения электронных оболочек и связанную с этой последовательностью периодичность св-в элементов. Макс. число электронов в оболочке с главным квантовым числом n определяется, согласно П. п., числом разл. наборов квантовых чисел l, m_l, и m_s, т. е. равно 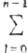2(2l + 1) = 2n². Отсюда получаются числа заполнения электронных оболочек в порядке возрастания номера оболочки: 2, 8, 18, 32 ... Для эквивалентных электронов атома, т. е. электронов с одинаковыми n и l, в силу П. п. осуществляются не все возможные состояния, а лишь те, к-рые различаются m_l или m_s. B частности, для электронной конфигурации (пр)² правило векторного сложения моментов кол-ва движения дает шесть термов: ^1,3S, ^1,3P ^1,3D, из к-рых разрешены только три: ¹S, ³P и ¹D, т. к. для остальных трех термов наборы квантовых чисел для двух электронов совпадают. Учет П. п. необходим также при нахождении разрешенных электронных состояний молекул и мол. комплексов. П. п. играет фундам. роль в квантовой теории твердого тела, теории ядерных реакций и р-ций между элементарными частицами.

Лит.: Ван-Дер-Варден Б., в сб.: Теоретическая физика 20 в., M., 1962, с. 231; Паули В., там же, с. 357; Каплан И. Г., "Успехи фнз. наук", 1975, т. 117, в. 4, с. 691--704; его же, в сб.: Теоретико-групповые методы в физике, т. 1, M., 1980, с. 175; Ландау Л. Д., Лифшиц E. M., Квантовая механика, 4 изд.. M., 1989. И. Г. Каплан.