Открытая система

ОТКРЫТАЯ СИСТЕМА, термодинамич. система, способная обмениваться с окружающей средой в-вом и энергией. Такой обмен может сопровождаться также изменением объема системы. В рамках статистич. термодинамики О. с. с фиксир. объемом принадлежит большому канонич. ансамблю, окружающая среда для системы является резервуаром энергии и частиц компонентов, т.е. определяет т-ру и хим. потенциалы компонентов и условия хим. и фазового равновесия, поведение р-ров и реальных газов (см. Статистическая термодинамика).

Изменение энтропии О. с. можно представить состоящим из двух частей, одна из к-рых (d_eS)обусловлена взаимод. с окружающей средой (в частности, теплообменом), а вторая (d_iS)- самопроизвольным протеканием необратимых "внутр." процессов в О. с.:

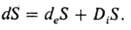
Согласно второму началу термодинамики, всегда 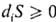(знак равенства относится к состоянию равновесия); d_eS не имеет определенного знака. Поэтому в принципе возможны процессы, при к-рых О. с. достигнет состояния с более низким значением энтропии по сравнению с начальным. Такие процессы имеют место, если поток энтропии из системы в окружающую среду превышает возникновение энтропии внутри О. с. В стационарном состоянии, при dS/dt= 0

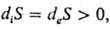
т.е. О.с. в стационарном состоянии как бы "насыщена" энтропией при заданных внеш. условиях. Постоянно возникающая в результате внутр. неравновесных процессов энтропия не может больше оставаться в О. с. и "вытекает" из нее в окружающую среду. Обычно это состояние трактуют таким образом, что в систему "втекает" отрицат. энтропия (него-энтропия). Стационарные неравновесные состояния О. с. характеризуются экстремальными значениями определенных функционалов. Согласно теореме Гленсдорфа-Пригожина, если в системе протекает неравновесный процесс, описываемый линейным ур-нием, то в стационарном состоянии скорость возникновения энтропии имеет миним. значение, совместимое с внеш. условиями для данной системы.

Диссипативные структуры. При поступлении в О. с. достаточно большого потока отрицат. энтропии в ней может поддерживаться нек-рая упорядоченность. Естественно, что "подпитка" отрицат. энтропией должна происходить в результате неравновесного процесса, в противном случае как d_iS/dt, так и d_eS/dt обратятся в нуль. Отсюда вытекает сформулированный И. Пригожиным основополагающий принцип, согласно к-рому неравновесные процессы в О. с. могут служить источником упорядоченности - самоорганизации. Возникшая упорядоченность принципиально отличается от упорядоченности при фазовых переходах, когда порядок возникает при понижении т-ры (типичный пример-кристалл). При неравновесных процессах в О. с. наблюдаются диссипативные структуры, т.е. состояния организации системы в пространстве, времени (или и в пространстве, и во времени), из к-рых система может перейти в состояние термодинамич. равновесия только путем скачка. По аналогии с термодинамич. фазовым переходом скачкообразное возникновение новых структур с др. св-вами симметрии наз. кинетич. фазовым переходом.

Диссипативные структуры могут возникать в физ., физ.-хим. и биол. О. с. при выполнении след. условий: 1) динамич. ур-ния, описывающие изменение состояния системы, нелинейны относительно соответствующих термодинамич. переменных; 2) отклонения от равновесных значений параметров состояния превышают нек-рые критич. значения; 3) мик-роскопич. процессы в системе происходят кооперативно (согласованно). Множественность решений нелинейных диф-ференц. ур-ний означает множественность стационарных состояний системы. Среди этих решений существуют динамически устойчивые и неустойчивые. Динамически устойчивым решениям соответствуют состояния, в к-рых малые флуктуации затухают и не могут перевести систему в новое состояние. Динамич. неустойчивость решения означает, что флуктуация спонтанно разрастается и система переходит в иное стационарное состояние. Оно может обладать более низкой симметрией, т.е. иметь более высокую степень упорядоченности. Т. обр., система с помощью флуктуации "выбирает" одно из возможных стационарных состояний, соответствующих устойчивому решению ур-ний макроскопич. процесса. Кооперативный (согласованный) характер поведения частиц в О. с. отражает причинность процессов самоорганизации на микроскопич. уровне. Только в том случае, если микроскопич. процессы в силу наличия механизмов обратной связи между ними согласованы, наблюдается спонтанное возникновение диссипативных структур. В О. с. известны след, диссипативные структуры: пространственно неоднородные; периодические во времени (автоколебания); пространственно-временные псриодич. структуры (автоволны); бистабильные структуры (типа триггера).

К наиб. важному типу О. с. относят системы с хим. р-циями, в к-рые непрерывно поступают извне реагирующие в-ва, а продукты р-ции отводятся. Эти системы можно описать с помощью т. наз. реакционно-диффузионной мат. модели Тьюринга, представляющей собой нестационарное ур-ние Фика для диффузии в сочетании с кинетич. ур-нием хим. р-ции как источника в-ва:

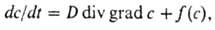
где с-концентрация компонента, D-коэф. диффузии, f(c)-нелинейная ф-ция, выражающая кинетику р-ции. Нелинейные дифференц. ур-ния могут иметь периодич. (автоко-лебат.) решение, проявляющееся в образовании предельного цикла, когда изменение состояния системы в фазовом пространстве представляет собой изолир. замкнутую траекторию, притягивающую к себе др. фазовые траектории. На практике автоколебат. характер хим. р-ций состоит в периодич. изменении концентраций промежут. в-ва. Наиб. изученной колебат. р-цией является Белоусова - Жаботинско-го реакция, динамич. поведение к-рой очень разнообразно (см. также Колебательные реакции).

Лит.: Смирнова Н.А., Методы статистической термодинамики в физической химии, М., 1973; Николис Г., Пригожин И., Самоорганизация в неравновесных системах, пер. с англ., М., 1979; ПолакЛ.С., Михайлов А. С., Самоорганизация в неравновесных физико-химических системах, М., 1983. Е. П. Агеев.