Оптимизация

ОПТИМИЗАЦИЯ (от лат. optimus-наилучший) в химической технологии. Под О. обычно понимают целе-направл. деятельность, заключающуюся в получении наилучших результатов при соответствующих условиях. Постановка задачи О. предполагает наличие ее объекта, набора независимых параметров (переменных), описывающих данную задачу, а также условий (часто наз. ограничениями), к-рые характеризуют приемлемые значения независимых переменных. Еще одной обязат. компонентой описания оптимизац. задачи служит скалярная мера "качества", носящая назв. критерия оптимизации, или целевой ф-ции, и зависящая к.-л. образом от переменных О. Решение оптимизац. задачи-это поиск определенного набора значений переменных, к-рому отвечает оптим. значение критерия О.

Некоторые основные понятия. Любой хим.-технол. процесс м.б. условно изображен так, чтобы были выделены осн. группы параметров, определяющих его течение и характеризующих состояние в любой момент времени (см. рис.). Как правило, выделяют след. группы:

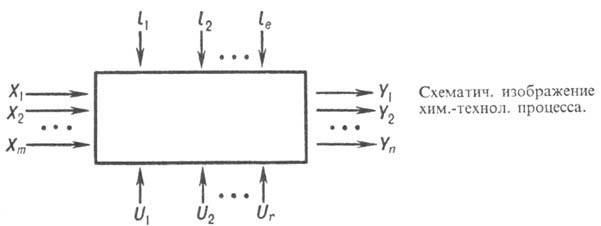
1) входные параметры X_i (i = 1, 2,..., m)-перемен-ные, значения к-рых можно измерить, но возможность воздействия на к-рые отсутствует. Пример - контролируемый состав исходного сырья, не поддающийся регулированию при эксплуатации хим. реактора.

2) Управляющие параметры Uj (j- 1, 2,..., r)-переменные, на к-рые можно оказывать прямое воздействие в соответствии с теми или иными требованиями, что позволяет управлять процессом. Такими регулируемыми параметрами для хим. реактора м. б., напр., кол-во подаваемой в него исходной смеси компонентов, давление, т-ра теплоносителя и т.д.

3) В о з м у щ а ю щ и е п а р а м е т р ы L_k (k = 1, 2, ..., e) - переменные, значения к-рых случайным образом изменяются во времени и к-рые недоступны для измерения имеющимися ср-вами. Примеры-разл. примеси в сырье, активность катализатора и др.

4) Выходные параметры Y_W (w = 1,2,..., n)-переменные, значения к-рых определяются режимом процесса и к-рые описывают его состояние, возникающее в результате суммарного воздействия входных, управляющих и возмущающих параметров (напр., характеристики получаемой продукции).

Совокупности перечисленных входных, выходных, управляющих и возмущающих параметров представляют собой соотв. векторы X, Y, U, L.

По отношению к анализируемому процессу, рассматриваемому без системы управления, входные и управляющие параметры можно считать внешними, что указывает на независимость их значений от режима процесса. Последний непосредственно влияет на выходные параметры, к-рые поэтому обычно определяются как внутренние. Возмущающие параметры могут относиться и к внешним, и к внутренним: напр., неконтролируемые примеси в сырье можно рассматривать как внеш. возмущающее воздействие, а изменение активности катализатора во времени-как внутр. возмущение.

Этапы постановки оптимизационной задачи. Для О. конкретной задачи хим. технологии необходимо: а) установить возможные границы изменения переменных; б) определить количеств. критерий О., на основе к-рого можно провести анализ вариантов с целью нахождения "наилучшего"; в) выбрать внутрисистемные переменные, используемые для определения характеристик и идентификации вариантов; г) построить модель, отражающую связи между переменными.

Если подлежащая исследованию хим.-технол. система определена и области изменения ее переменных установлены (первый этап), осуществляют выбор критерия О., посредством к-рого можно оценить характеристики системы или ее проекта для выявления "наилучшего" варианта проекта либо "наилучших" условий функционирования системы (второй этап). В общем случае критерий О. обычно представляют как ф-цию входных, выходных и управляющих параметров 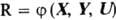. Наиб. часто выбирают критерии экономич. характера (напр., валовые капитальные затраты, чистая прибыль в единицу времени, отношение затрат к прибыли и т.д.). Кроме них м.б. использованы также технол. критерии (напр., требуется минимизировать продолжительность произ-ва изделия, максимизировать нагрузку на реактор, минимизировать кол-во потребляемой электроэнергии). Независимо от того, какой критерий выбирают при О. данного объекта, "наилучшему" варианту всегда соответствует "минимальное" или "максимальное" значение критерия.

При решении задачи О. можно применять только один критерий, поскольку невозможно получить решение, к-рое обеспечивает одновременно, напр., минимум затрат, максимум надежности оборудования и минимум потребляемой энергии. Если все же конкретная задача О. характеризуется совокупностью неск. критериев (часто при этом противоречивых), то один из путей ее решения заключается в выборе к.-л. критерия в качестве первичного, в то время как остальные критерии будут вторичными. Обычно О. используют первичный критерий; вторичные критерии рассматриваются как ограничения оптимизац. задачи, к-рые должны выполняться для решения задачи О.

На третьем этапе постановки задачи осуществляют выбор независимых переменных, к-рые позволяют адекватно оценивать качество проекта или условия функционирования системы. На этом этапе проводят различие между переменными, значения к-рых могут изменяться в достаточно широком диапазоне, и переменными, значения к-рых фиксированы и определяются внеш. факторами. Кроме того, выявляют различие между теми параметрами, к-рые могут предполагаться постоянными, и параметрами, подверженными флук-туациям вследствие воздействия неконтролируемых факторов. На данном этапе необходимо учесть все наиб. важные переменные, от к-рых зависит функционирование системы или качество проекта, но не "перегружать" оптимизац. задачу большим числом мелких, несуществ. деталей.

После того как критерий О. и переменные задачи выбраны, на четвертом этапе нужно построить модель, к-рая описывает связи между переменными и их влияние на критерий О. В принципе она м.б. выполнена на основе непосредств. экспериментирования с системой путем поиска значений управляющих воздействий, при к-рых выбранный критерий О. имеет наилучшее значение. Однако на практике чаще используют мат. модель объекта О. (см. Моделирование). Применение мат. моделей предпочтительнее, поскольку опыты, проводимые на реальных системах, требуют, как правило, больших затрат ср-в и времени, а в ряде случаев связаны с значит. риском.

Мат. модель представляет собой систему ур-ний, отражающую сущность явлений, протекающих в объекте моделирования, решение к-рой с помощью определенного алгоритма позволяет прогнозировать поведение объекта при изменении входных и управляющих параметров. В самом общем виде структура модели включает осн. ур-ния материальных и энергетич. балансов, соотношения, связанные с проектными решениями, а также ур-ния, к-рые описывают физ. процессы, протекающие в системе. Эти ур-ния обычно дополняют неравенствами, к-рые определяют область изменения значений независимых переменных, позволяют сформулировать требования, накладываемые на границы изменения характеристик функционирования системы, и т.д.

Классификация оптимизационных задач. В общем случае задачу О. объектов хим. технологии можно представить как задачу минимизации или максимизации веществ, ф-ции мн. переменных f(x), где х- вектор с компонентами x_i-. Последние представляют собой совокупность всех переменных объекта, изменяемых при его О. На эти переменные в общем случае м.б. наложены дополнит. условия в форме равенств, неравенств, а также двусторонних ограничений сверху и снизу:

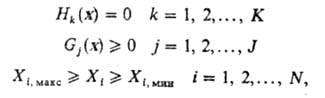
где H_k(x), С_j(x) - веществ, нелинейные ф-ции векторного аргумента \, К, J, N~ число условий соответствующих типов. При этом обычно ф-цию f(x) наз. целевой, ур-ния H_k(х) = 0-ограничениями в виде равенств, а неравенства G_j(x)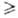0-ограничениями в виде неравенств.

Задачи общего вида: минимизировать (максимизировать) f(x) при указанных ограничениях, наз. оптимизац. задачами с ограничениями, или задачами условной О. Задачи, в к-рых ограничения отсутствуют, носят назв. задач без ограничений, или задач безусловной О. Последние особенно важны, поскольку мн. методы решения условных задач основаны на сведении их к безусловным.

Оптимизац. задачи классифицируют также в соответствии с видом ф-ций f(x), H_k(х)и G_j(x). Ф-ции мн. переменных наз. линейными, если все их частные производные 1-го порядка не зависят от переменных, в противном случае - нелинейными. Задачи, в к-рых все указанные ф-ции линейны, относят к задачам линейного программирования. Если среди пере-числ. ф-ций хотя бы одна нелинейна, то такие задачи обычно относятся к задачам нелинейного программирования. (Термин "программирование" в данном случае не связан непосредственно с программированием ЭВМ, а означает лишь определенную процедуру решения задачи.)

Для задач линейного программирования разработаны эффективные алгоритмы, позволяющие находить оптим. решение за конечное число шагов, т. е. вычислений значений критерия О. Задачи нелинейного программирования решают обычно методом последоват. приближений, при этом точность получаемых решений зависит от числа выполненных шагов; поэтому для таких задач разработан ряд спец. методов, использующих конкретные особенности критерия О. и ограничений (напр., квадратичное или динамич. программирование, принцип максимума и т.д.).

Подготовка задач к решению и оптимизационные расчеты.

При наличии модели, отражающей связи между переменными оптимизируемого объекта, следует подготовить задачу к решению с помощью подходящего алгоритма О., к-рый позволяет найти решение задачи с заданной точностью за конечное число шагов.

Вычислит. трудности, связанные с решением оптимизац. задачи, м.б. обусловлены след. причинами: 1) плохим масштабированием переменных, что проявляется как-большое различие в чувствительности критерия О. к изменениям разных переменных; 2) неудачным выбором метода О.; 3) неудачным выбором начального приближения решения.

В качестве метода О. обычно выбирают метод, к-рый приводит к конечным результатам с наим. затратами на вычисления. Выбор того или иного метода в значит. степени определяется постановкой оптимизац. задачи, а также используемой мат. моделью объекта О.

О. широко используют в хим. технологии для проектирования новых и интенсификации действующих процессов и произ-в. Примеры типовых задач О.: оптим. распределение технол. параметров (нагрузок, давлений, т-р и др.) в хим. реакторах; О. каскада аппаратов (теплообменников, дистилляц. колонн, реакторов и т.д.); О. хим.-технол. схем (ХТС) как сложных систем взаимосвязанных аппаратов; синтез оптим. структур ХТС при создании новых произ-в.

Лит.: Бояринов А. И., Кафаров В. В., Методы оптимизации в химической технологии, 2 изд., М., 1975; Химмельблау Д., Прикладное нелинейное программирование, пер. с англ., М., 1975; Химический энциклопедический словарь, М., 1983; Островский Г. М., Бережинский Т. А., Оптимизация химико-технологических процессов. Теория и практика, М., 1984; Гилл Ф., Мюррей У., Райт М., Практическая оптимизация, пер. с англ., М., 1985; Оптимизация качества. Сложные продукты и процессы, М., 1989.

Я. С. Кондаков.