Молекулярная динамика

МОЛЕКУЛЯРНАЯ ДИНАМИКА, изучает вращательное и поступательное (трансляц.) движение молекул, а также внутримолекулярные движения: колебания атомов и атомных групп, конформац. перестройки, вращения отдельных мол. фрагментов и т. п. Характерные времена этих движений зависят от структуры молекул, их окружения, плотности в-ва, т-ры и др. термодинамич. параметров и изменяются от ~10^-14 с (внутримолекулярные колебания и вращение малых молекул) до 10⁴ с (конформац. перестройки молекул в твердых телах). Амплитуды соответствующих мол. движений малы и, как правило, не превышают 1 нм.

Эксперим. исследование мол. движений проводят с па-мощью ЯМР, ЭПР, оптич. спектроскопии (люминесцентной, ИК, комбинац. рассеяния), методов диэлектрич. и мех. релаксаций, рассеяния нейтронов, рентгеновских лучей и др.; для интерпретации результатов привлекают модельные представления о мол. структуре изучаемого объекта и динамике молекул. Из теоретич. методов в первую очередь используют моделирование мол. структур на ЭВМ-ч и сл е н н ы е э к с п е р и м е н т ы (часто наз. также м а ш и н н ым и или в ы ч и с л и т е л ь н ы м и э к с п е р и м е н т а м и). Такое моделирование основано на определенных физ. гипотезах относительно характера движения частиц в системе, их взаимод. и т. п.; оно позволяет провести детальный анализ динамич. св-в разл. мол. систем, зависимость этих св-в от т-ры и др. термодинамич. параметров и влияния динамики молекул на макроскопич. св-ва в-ва. Одно из существ. достоинств численных экспериментов - возможность проверить исходные физ. гипотезы и вычислит. методики, оставаясь в рамках самих этих экспериментов. Совр. ЭВМ позволяют проводить численные эксперименты для систем с относительно небольшим числом N частиц (как правило, N = 10²-10³). Поэтому для моделирования изотропных макроскопич. систем часто полагают, что все пространство заполнено тождеств. ячейками с периодич. граничными условиями (напр., кубич. ячейками, когда считаются тождественными противоположные грани). .

В М.д. используют разл. численные эксперименты. Одна группа методов исследует возможности внутри- и межмол. движений на основе расчета геом. и энергетич. характеристик молекул в равновесном состоянии (см. Молекулярная механика). В т.наз. м о л е к у л я р н о-д и н а м и ч е с к и х э к сп е р и м е н т а х (МДЭ) непосредственно моделируется мол. движение. Частицы (отдельные атомы, атомные группы, небольшие молекулы) представляются материальными точками; потенциалы межмол. взаимод. задаются в явном виде. При этом обычно используют геом. (жесткие) связи и модельные потенциалы парного взаимод.; иногда применяют и потенциалы многочастичного взаимод., а также рассчитанные квантовомеханически. Для определения траектории частиц используют разл. ур-ния. В т.наз. м е т о д е м о л е к у л я р н о й д и н а м и к и (МД) интегрируют ур-ния движения классич. механики:

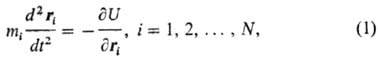
где N-число частиц, U-потенц. ф-ция взаимод., t-время, r_i и т_i-соотв. радиус-вектор и масса i-й частицы. Для интегрирования системы ур-ний (1) необходимо задать начальные координаты и импульсы частиц и граничные условия. Чтобы рассчитать термодинамич. параметры системы (т-ру, давление или тензор напряжений), используют э р г о д и ч е с к у ю г и п о т е з у, согласно к-рой средние по фазовой траектории (в пространстве координат и импульсов) значения параметров совпадают со средними по ансамблю. Аналогично определяют структурные параметры системы (напр., парные ф-ции распределения) и динамич. характеристики (временные корреляц. ф-ции смещений частиц, их скоростей, действующих на них сил и др.). Метод МД позволяет изучать также влияние внеш. полей (мех., электрич.) на мол. системы, для чего вводятся спец. граничные условия, к-рые могут зависеть от времени (т. наз. неравновесный метод МД).

Пространственные и временные ограничения метода МД связаны с возможностями используемых ЭВМ, размером и структурой принимаемых мол. моделей. В первых работах (Б. Олдер, Т. Вайнрайт, 1959) расчеты выполнялись для двухмерной модели жидкости из неск. десятков частиц. Совр. ЭВМ позволяют рассчитывать фазовую траекторию для систем из 10³-10⁶ атомов за времена ~ 10^-10 с. Даже в рамках этих ограничений метод МД успешно используют для решения мн. вопросов мол. физики конденсир. состояния в-ва. Так, установлено, что диффузионный процесс в простых жидкостях и воде осуществляется не скачкообразными перемещениями отдельных молекул из одного положения относит. равновесия в другое, а благодаря коллективным непрерывным движениям всей совокупности молекул. Метод МД позволяет понять механизм образования кристаллич. дефектов под воздействием ионизирующих излучений, термич. и мех. нагружения. Этот метод используют для изучения аморфных металлов, стекол, полимеров, белковых молекул, для объяснения адсорбц. понижения прочности (эффекта Ребиндера).

В методе б р о у н о в с к о й д и н а м и к и (БД) для описания движения частиц используют у р-н и е Л а н ж е в е н а:

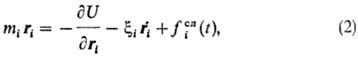
где x_i-т. наз. коэф. трения i-й частицы, связанный с диссипацией мех. энергии, f_i^сл(t)-действующая на частицу в момент времени t случайная сила, возникающая из-за взаимод. рассматриваемых частиц с окружающими молекулами среды. Метод БД позволяет рассчитывать траектории частиц в плотных газах и жидкостях. Объем требуемых вычислений существенно уменьшается по сравнению с методом МД, поскольку молекулы среды не принимаются во внимание. Кроме того, метод БД позволяет рассмотреть мол. динамику за большие промежутки времени или анализировать более объемные структуры. Его применяют для анализа систем, в к-рых достаточно крупные частицы подвержены броуновскому движению (напр., золей), а также для исследования динамики макромолекул в р-рах и расплавах полимеров.

Для вычисления траекторий частиц используют и др. ур-ния движения, в к-рых случайное действие окружающей среды на рассматриваемую систему вводится иначе, чем в ур-нии (2). Все они являются вариантами обобщенного ур-ния Ланжевена, учитывающего временные и пространств. корреляции случайных сил и сил трения (т. наз. методы ланжевеновой динамики). Используя разл. упрощающие предположения, можно построить определенную иерархию приближений, к-рая позволяет рассматривать мол. систему в разных временных масштабах (см., напр., Динамика элементарного акта хим. р-ции).

М е т о д М о н т е-К а р л о (ММК) позволяет оценивать динамич. св-ва системы на основе данных о ее своб. энергии. При этом для решения задач М.д. используют известный метод вычислит. и прикладной математики, наз. методом статистич. испытаний. Его широко применяют в физ. химии при изучении структурных параметров и термодинамич. св-в равновесных неупорядоченных или частично упорядоченных мол. систем (плотных газов, мол. жидкостей, расплавов солей и металлов, жидких кристаллов, р-ров и расплавов полимеров). Для расчетов обычно используют схему Метро-полиса, согласно к-рой рассматривается система частиц с заданными значениями потенц. энергии взаимод., к-рые зависят только от координат частиц. В классич. схеме Метрополиса переход от одного расположения частиц с. потенц. энергией (потенциалом) U к другому (потенциал U')происходит с вероятностью 1, если U' >= U, и вероятностью exp(U' — U)/kT, если U' < U (T-абс. т-ра, k-постоянная Больцмана). Тем самым моделируется канонич. статистич. ансамбль, для к-рого можно вычислить термодинамич. средние (энергии Гиббса и Гельмгольца, энтропии), структурные параметры и др.

Для решения задач М.д. методом Монте-Карло применяют аналогичную схему моделирования ансамбля взаимод. частиц. Благодаря использованию достаточно реалистич. потенц. ф-ций взаимод. были получены важные сведения о локальных мол. структурах - вблизи межфазных границ, ионных оболочек расплавов солей и орг. молекул и др.; изучается мол. структура воды, конформации макромолекул в р-рах, расплавах и около пов-стей разной формы и т. п. ММК позволяет определить вероятность разл. равновесных конфигураций молекул и оценить подвижность молекул при разных т-рах: найти средние значения амплитуды колебаний атомов, валентных и торсионных углов, определить возможные пути внутри- и межмол. перестроек.

В динамич. методе Монте-Карло (ДММК) последовательность координат частиц, получаемых при расчете по ММК, рассматривается в качестве их временных траекторий. Для этого необходимо при обработке результатов определить физ. время, т. к. в самом ММК оно отсутствует. Время можно ввести, напр., с помощью соотношения Эйнштейна L² ~ Dt, где D-коэф. мол. диффузии, L-среднее смещение частиц за время t, или на основе другого наблюдаемого в системе процесса, для к-рого известны (из теории, численного или физ. эксперимента) временные параметры (среднее время внутримолекулярных перестроек, времена к.-л. релаксац. процессов). В отличие от упомянутых выше методов МДЭ, рассматриваемый вариант ДММК в результате огрубления мелкомасштабных движений позволяет исследовать динамику молекул на больших временных масштабах - вплоть до времен макроскопич. процессов. Однако методика его проведения в каждом конкретном случае требует спец. обоснования. ДММК используют для анализа релаксац. процессов в полимерных системах и полиэлектролитах, изучения мех. св-в мол. сеток, исследования влияния диффузии и ближнего окружения реагирующих частиц ("изоляции") на кинетику хим. р-ций и др.

Лит.: Крокетон К. А., Физика жидкого состояния, пер. с англ., М., 1978; Федосеев Д. В., Чужко Р. К., Гривцов А. Г., Гетерогенная кристаллизация из газовой фазы. Вопросы кинетики и численное моделирование, М., 1978; Лагарьков Л. Н., Сергеев В. М., Метод молекулярной динамики в статистической физике, "Успехи физ. наук", 1978, т. 125, в. 3, с. 409-48; Методы Монте Карло в статистической физике, пер. с англ., М., 1982; Орлов А. Н., Трушин Ю. В., Моделирование на ЭВМ радиационных дефектов и процессов в кристаллах, "Природа", 1983, № 10, с. 34-43; Лихтенберг А., Либер-ман М., Регулярная и стохастическая динамика, пер. с англ., М., 1984; Готлиб Ю. Я., Даринский А. А., Светлов Ю. Е., Физическая кинетика макромолекул, Л., 1986. М.А.Мазо.