Мембранный потенциал

МЕМБРАННЫЙ ПОТЕНЦИАЛ, разность электрич. потенциалов между р-рами электролитов a и b, разделенных проницаемой мембраной m: D^a_bj = j^a - j^b. В частном случае, когда мембрана проницаема только для определенного иона В^zв (z_B - зарядовое число), общего для р-ров электролитов a и b, М.п. (иногда его наз. потенциалом Нернста) рассчитывают по ф-ле:

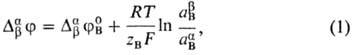
где F-число Фарадея, R-газовая постоянная, Т-абс. т-ра, a_B^b, a_B^a - активности иона В в р-рах b и a, D^a_bj_B-стандартный потенциал распределения иона В, равный

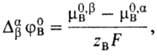
где m^0,b_B, m^0,a_B-стандартные хим. потенциалы иона В в р-рах b и a соответственно. В такой системе М.п. не зависит от толщины мембраны и ее структуры, механизма переноса иона и его подвижности.

В общем случае для мембран, проницаемых для одних сортов ионов и не проницаемых для других, при расчете М.п. требуется введение определенных приближений в зависимости от толщины мембраны, ее состава и строения, а также от механизма переноса. В случае мембран макро-скопич. размера полный М.п. слагается из трех компонентов: двух граничных потенциалов, локализованных в двойных электрич. слоях на границе мембрана-р-р электролитов, и внутримембранного, локализованного в электронейтральном объеме мембраны. Кроме того, при пропускании электрич. тока через мембрану внутри нее возникает падение напряжения. Обычно считается, что переход ионов через межфазную границу происходит быстро, так что их распределение равновесно; затруднен только перенос ионов через объем мембраны. Для системы, в к-рой в фазе a имеется бинарный электролит В⁺ А^-, присутствующий и в мембране, а мембрана содержит ион R с зарядовым числом z_R, не проникающий через межфазные границы, граничный потенциал определяется ф-лой Доннана и наз. д о н н а н о в с к и м:

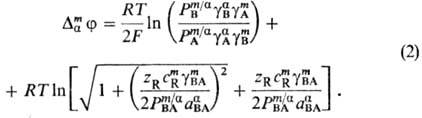
Здесь c^m_R - концентрация ионов R в мембране, g_i- и Р_i-коэф. активности и распределения ионов соотв., определяемые соотношением

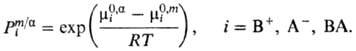
Средняя активность электролита 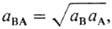средний коэф. активности 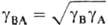, коэф. распределения электролита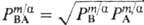

Т. обр., доннановский потенциал (2) состоит из т. наз. потенциала распределения и члена, зависящего от концентрации непроникающего иона R; при малом значении c^m_R он сводится к потенциалу распределения, а при большом-находится из выражения:

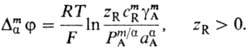
При этом концентрация противоионов А^- в мембране перестает зависеть от коэф. распределения и межфазного потенциала и приближается к предельному значению c^m_A 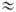z_Rc^m_R, a одноименно заряженные ионы почти полностью вытесняются из мембраны.

Граничный потенциал может возникнуть в результате р-ций комплексообразования или электронообменной р-ции между окислит.-восстановит. парами, содержащимися в р-ре и в мембране. Если межфазная граница вообще не проницаема для заряженных частиц, граничный потенциал имеет электростатич. природу и возникает в результате адсорбции зарядов и диполей, а также вследствие заряжения границы от внеш. источника.

Внутримембранный потенциал имеет кинетич. природу и определяется переносом ионов через толщу мембраны. В простейшем случае при диффузионно-миграц. переносе бинарного электролита возникает т. наз. диффузионный потенциал (приближение Планка):

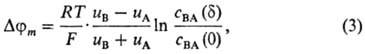
где u_А, u_B-подвижности ионов в мембране, c^m_BA(0), c^m_BA(d)-концентрации электролита в мембране у левой и правой межфазных границ соответственно. В случае биол. и бислой-ных липидных мембран, толщина к-рых настолько мала, что в них вообще не реализуется область электронейтральности, для нахождения внутримембранного потенциала используют предположение о постоянстве напряженности электрич. поля (приближение Гольдмана):

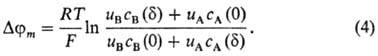
Т. обр., М.п. в доннановском случае находят из выражения, слагаемые к-рого определены ф-лами (2) и (3) или (2) и (4):

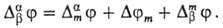
Определение М. п. представляет интерес для ионометрии, для биологии и медицины в связи с распространенностью мембранных процессов в живых организмах и т.д.

Лит.: Феттер К., Электрохимическая кинетика, пер. с нем., М., 1967; Маркин В. С., Чизмаджев Ю. А., Индуцированный ионный транспорт, М., 1974; Лакшминараянайах Н., Мембранные электроды, пёр. с англ., Л., 1979; Морф В., Принципы работы ионоселективных электродов и мембранный транспорт, М., 1985; Маркин B.C., Волков А. Г., "Успехи химии", 1988, т. 57, № 12, с. 1963-89; Lakshminarayanaiah N., Transport phenomena in membranes, N.Y.-L., 1969. Ю.А. Чизмаджев.