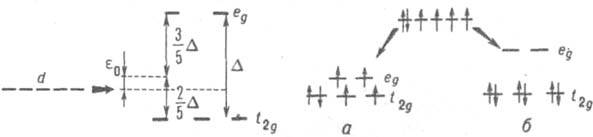КРИСТАЛЛИЧЕСКОГО ПOЛЯ ТЕОРИЯ, квантовохим. теория, в к-рой низшие по энергии состояния молекулы описываются как состояния одного атома (иона), находящегося в электростатич. поле, созданном остальными частицами. Как правило, К. п. т. применяется к координац. соед., кристаллам и др. системам, в структуре к-рых можно выделить центр. атом и окружающие его ионы или молекулы (в случае координац. соед. -лиганды). Лиганды моделируют системой точечных зарядов или диполей, а создаваемое ими электростатич. поле рассматривают по аналогии с внутрикристаллич. полем, к-рое обусловлено положит. и отрицат. зарядами ионов в кристалле. Поэтому такое приближение наз. теорией кристаллич. поля.
В рамках К. п. т. предполагается, что энергия электронного возбуждения лигандов намного больше, чем энергия возбуждения центр. атома, а взаимод. лигандов и центр. атома не очень сильно. Поэтому низшие по энергии электронные состояния комплекса в целом рассматривают как состояния центр. атома (иона), изменившиеся по сравнению с состояниями своб. атома под действием электростатич. поля лигандов. Эти изменения оценивают методами возмущений теории. К. п. т. позволяет установить относит. положение энергетич. уровней и энергии переходов между ними для молекулы или кристалла при заданном расположении лигандов в пространстве, изучить изменение энергетич. уровней при замещении лигандов или центр. атома, при изменении геом. строения комплекса, появлении на пов-сти кристалла адсорбир. частиц и др.
Электронное строение атомов или ионов в кристалле и мол. комплексах определяется мн. факторами, среди к-рых К. п. т. выделяет два: энергия взаимод. лигандов с центр. атомом и энергия межэлектронного отталкивания, характеризующая состояние валентных электронов центр. атома. Характерное для атома в данной степени окисления отталкивание электронов не меняется в разных комплексах, а интенсивность поля лигандов возрастает в экспериментально установленном (т. наз. спектрохим.) ряду: I-<Вr-<Сl-<F-<ОН-<Н2О<NH3<NO2-<CN-, что позволяет различить два предельных случая: 1) слабое поле: межэлектронное отталкивание намного больше, чем воздействие поля лигандов. В этом случае за основу берут детально изученные спектроскопич. методами состояния многоэлектронного атома, а влияние лигандов учитывают с
помощью теории возмущений. 2) Сильное поле: воздействие лигандов на центр. атом больше, чем влияние межэлектронного отталкивания. В этом случае сначала изучают состояния отдельных электронов атома в поле лигандов, а затем учитывают поправки на межэлектронное взаимодействие. Оба подхода были бы эквивалентны, если бы ур-ние Шрёдингера для атома в поле лигандов решалось точно, однако при приближенном решении этого ур-ния с учетом наиб. важных вкладов в энергию физически правильное описание каждого комплекса дает, как правило, лишь один из подходов.
Для свободного сферически симметричного атома обычно имеет место вырождение энергетических уровней, поэтому для качеств. анализа в рамках К. п. т. достаточно учесть симметрию расположения лигандов (следовательно, симметрию создаваемого ими поля) и методами теории групп описать снятие вырождения под действием поля лигандов. Особенно просто выполнить анализ, рассматривая состояния отдельных электронов в атоме. Напр., комплекс [Fe(CN)6]4- имеет октаэдрич. строение, а своб. иону Fe2+ отвечает электронная конфигурация d6. Вырождение пяти d-орбиталей иона снимается частично в октаэдрич. поле (рис. 1), что приводит к образованию двукратно вырожденного уровня еg и трехкратно вырожденного уровня t2g. Расчет методами теории групп показывает, что если за начало отсчета энергии принять энергию d-уровня, то энергии уровней ед и t2g равны соотв. e0+3/5D и e0-2/5D, где e0 - изменение энергии d-уровня под действием сферически симметричной части поля лигандов, а D - энергия перехода между уровнями еg и t2g. Поле лигандов CN- достаточно сильное, и в первом приближении взаимод. электронов можно пренебречь, т.е. считать, что электронная конфигурация иона Fe2+ в комплексе для основного состояния t62g (рис. 2); основное состояние иона в комплексе полносимметрично и отвечает нулевому суммарному спину (состояние 1А1g). Комплекс [Fe(H2O)6] также имеет октаэдрич. структуру, и снятие вырождения d-уровней своб. атома можно описать рис. 1, однако поле лигандов гораздо слабее. В этом случае при заполнении электронами уровней необходимо учитывать, что величина А мала по сравнению с межэлектронным отталкиванием, т. е. использовать правило Хунда (см. Мультиплетность). Основное состояние комплекса отвечает тогда заполнению уровней, к-рое приводит к максимально возможной мультиплетности системы, равной 5 (рис. 2, а). Рассмотренная ситуация характерна для мн. комплексов: в случае сильного поля комплексы обычно являются низкоспиновыми, в случае слабого поля - высокоспиновыми. Использование сведений о состояниях отдельных электронов в атоме не является необходимым в К. п. т., т.к. эти состояния определены лишь в приближениях типа молекулярных орбиталей методов, а теоретич. методы К. п. т. можно применять непосредственно к состояниям атома как целого. Напр., своб. ион Fe2+ имеет основное состояние типа 5D. Под действием слабого поля лигандов суммарный спин не меняется, а снятие пятикратного
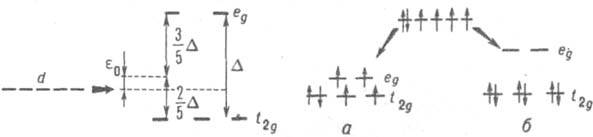Рис. 1. Снятие вырождения d-уровней в поле октаэдрич. симметрии.
Рис. 2. Основное состояние атома с электронной конфигурацией d6 в октаэдрич. поле лигандов в случае слабого поля (а) и сильного поля (б).
вырождения D-уровней атома описывается теми же законами, что и снятие вырождения одноэлектронных d-уровней. В поле октаэдрич. симметрии D-уровни расщепляются на уровни типов Еg и T2g, т.е. низшие состояния иона Fe2+ в слабом октаэдрич. поле лигандов 5Еg и 5T2g.
наиб. сложны для анализа случаи среднего поля, когда необходимо одновременно учитывать и межэлектронное взаимод., и влияние поля лигандов. В подобных случаях используют результаты модельных расчетов в виде таблиц или диаграмм (напр., т. наз. диаграмм Танабе-Сугано) или экстраполируют результаты расчетов, сделанных для предельных случаев слабого и сильного поля.
Применение К. п. т. ограничено системами, в к-рых центр. атом слабо влияет на лиганды и не образует с ними прочных связей. В противном случае необходимо учитывать изменения состояний лигандов (см. Поля лигандов теория). Благодаря ясному физ. смыслу и простоте оценок, основанных на законах симметрии, К. п. т. применяется для интерпретации оптич. и ЭПР-спектров мол. комплексов и кристаллов, при анализе строения координац. соед., устойчивости ионов в р-рах, каталитич. активности и др.; особенно широко ее используют применительно к соединениям элементов с незаполненными полностью d- или f-оболочками.
К. п. т. развита X. Бете (1929) для изучения спектральных характеристик кристаллов.
Лит.. Берсукер И. Б., Электронное строение и свойства координационных соединений, 2 изд., Л., 1976; Свиридов Д. Т.. Смирнов Ю. Ф.. Теория оптических спектров ионов переходных металлов, М., 1917. В, И. Пупышев.
