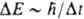КВАНТОВЫЕ ПЕРЕХOДЫ, скачкообразные изменения квантового состояния микрообъектов. Излучат. К. п. характеризуются изменением энергии системы в результате поглощения либо испускания квантов электромагн. излучения. Безызлучат. К. п. связаны с перераспределением энергии между разл. подсистемами квантовой системы (напр., подсистемами ядер и электронов молекулы), а также с переносом энергии от квантовой системы к окружению, к-рое может не рассматриваться как часть квантовой системы. При этом подразумевается, что перенос энергии не сопровождается ее выделением или поглощением в виде электромагн. излучения.
Осн. характеристики К. п. - вероятность перехода, равная числу переходов в единицу времени (1 с), и время жизни квантового состояния, участвующего в переходе. Если система может претерпевать неск. К. п., как излучательных, так и безызлучательных, то полная вероятность изменения состояния системы равна сумме вероятностей К. п. разл. типов. Временем жизни k-гo состояния tК наз. средняя продолжительность пребывания системы в этом состоянии. Чем меньше время жизни данного состояния, тем больше вероятность перехода системы из этого состояния в другие. Система, в к-рой происходит К. п., заведомо находится в нестационарном состоянии и описывается с помощью временного ур-ния Шрёдингера (см. Квантовая механика). В силу соотношения неопределенностей между энергией и временем квантовая система в возбужденном состоянии имеет конечную ширину энергетич. уровня 
, где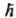 
-постоянная Планка, Dt - характерное время состояния. В уширение уровня вносят вклад как излучат., так и безызлучат. К. п. Если предположить, что ширина уровня DE мала по сравнению с энергией 
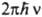кванта излучения (v-частота), К. п. можно наглядно интерпретировать как переход между стационарными энергетич. состояниями системы.
Излучательные К. п. изучаются методами спектроскопии. Положение спектральной линии характеризует энергию перехода, а интенсивность и ширина линии - вероятность перехода. Совокупность всех параметров, определяющих взаимод. молекулы с излучением и связанных с интенсивностями спектральных линий, наз. радиац. характеристиками молекулы. В качестве радиац. характеристик
используются коэффициенты Эйнштейна, сила осциллятора, вероятности переходов (см. ниже).
Излучат. К. п. могут быть спонтанными и вынужденными. Спонтанное излучение (испускание) происходит независимо от внеш. воздействия на мол. систему. Вероятность спонтанного излучения, сопровождающегося испусканием квантов электромагн. энергии и переходом мол. системы с n-го энергетич. уровня на m-й, характеризуется коэф. Эйнштейна Апm - средним числом квантов, испускаемых системой за 1 с и отнесенных к числу молекул в системе. Вероятность поглощения и вынужденного испускания зависит от плотности электромагн. излучения и характеризуется коэф. Эйнштейна Вmn и Впт, равными соотв. числу квантов электромагн. поля, к-рое поглощается или вынужденно испускается системой в среднем в расчете на 1 молекулу за 1 с при единичной плотности излучения. Связь между коэф. Аnт, Втп, Вnm была получена А. Эйнштейном на основе термодинамич. рассмотрения и впоследствии строго обоснована в квантовой электродинамике. Она выражается соотношениями:
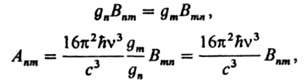
где gn(gт) - кратность вырождения энергетич. уровня n(m), с-скорость света. В мол. спектроскопии в качестве радиац. характеристики часто используется сила осциллятора fmn ~ vmnBmn. Коэф. Эйнштейна и силу осциллятора для мол. системы можно рассчитать, если известны волновые ф-ции исходных и конечных энергетич. состояний и оператор момента перехода
:
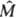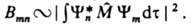
Роль оператора момента перехода
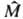в наиб. типичных случаях играет оператор электрического дипольного момента.
Излучат. К. п. классифицируют по типам квантовых состояний, между к-рыми происходит переход. Электронные К. п. обусловлены изменением электронного распределения - переходами внеш. (валентных) электронов между орбиталями (типичные энергии DEnm ~ 2,6.105 Дж/моль, частоты излучения лежат в видимой и УФ областях спектра), ионизацией внутр. электронов (для элементов с зарядом ядра Z ~ 10 DЕпт ~ 1,3.108 Дж/моль, излучение в рентгеновском диапазоне), аннигиляцией электроннопозитронных пар (DЕnm ~ 1,3.1011 Дж/моль, излучение в g - диапазоне). При переходах из возбужденных электронных состояний в основное различают флуоресценцию (оба состояния, связанные К. п., имеют одинаковую мультиплетность) и фосфоресценцию (мультиплетность возбужденного состояния отличается от мультиплетности основного) (см. Люминесценция). Колебат. К. п. связаны с внутримол. процессами, сопровождающимися перестройкой ядерной подсистемы (DEmn ~ 1.103-5.104 Дж/моль, излучение в ИК диапазоне), вращат. К. п.-с изменением вращат. состояний молекул (10-10-2 см-1 ~ 1,2.102-1,2310-1 Дж/моль, излучение в микроволновой и радиочастотной областях спектра). Как правило, в мол. системах при электронных К. п. происходит изменение колебат. состояний, поэтому соответствующие К. п. наз. электронно-колебательными. Отдельно выделяют К. п., связанные с изменением ориентации спина электрона или атомных ядер (эти переходы оказываются возможными благодаря расщеплению энергетич. уровней системы в магн. поле), изменением ориентации квадрупольного электрич. момента ядер в электрич. поле. Об использовании указанных К. п. в хим. анализе и для изучения структуры молекул см. Вращательные спектры, Колебательные спектры, Электронные спектры. Мёссбауэровская спектроскопия, Электронный парамагнитный резонанс, Ядерный магнитный резонанс, Ядерный квадруполъный резонанс, Рентгеновская спектроскопия, Фотоэлектронная спектроскопия.
Помимо обычных одногвантовых переходов, в каждом из к-рых поглощается или испускается один квант энергии, возможны многофотонные процессы, представляющие собой либо последовательность неск. одноквантовых переходов, либо один К. п. системы между двумя квантовыми состояниями, но с излучением или поглощением неск. квантов одинаковой или разной энергии. Вероятность многоквантовых переходов быстро уменьшается с понижением интенсивности взаимодействующего с в-вом электромагн. излучения, поэтому их исследование стало возможным лишь благодаря применению лазеров. Простейший двухквантовый процесс - комбинац. рассеяние света, при к-ром частица (атом, молекула) одновременно поглощает квант энергии и испускает квант меньшей или большей энергии. При последоват. поглощении молекулой двух квантов света возможны в ряде случаев фотохим. р-ции (см. Двухквантовые реакции). Четырехквантовый переход является, напр., основой метода когерентного антистоксова рассеяния света (КАРС) (см. Комбинационного рассеяния спектроскопия). С помощью этого метода удается изучать такие состояния, переходы в к-рые запрещены при одноквантовых переходах.
Приближенная трактовка излучат. К. п. как переходов между стационарными состояниями системы справедлива только в случае взаимод. квантовых систем со слабым электромагн. полем. В сильных полях само понятие "уровень энергии квантовой системы" не м. б. определено. Для сильных периодич. полей вводится концепция ква-зиэнергетич. состояний, в рамках к-рой можно описывать изменения, происходящие с системой при взаимод. с полем.
Если квантовая система состоит из большого числа одинаковых подсистем, возможна синхронизация излучат. К. п. в разл. подсистемах, приводящая к возникновению когерентного излучения. Данное явление лежит в основе работы лазеров и др. квантовых генераторов излучения.
В результате излучат. К. п. система может остаться существовать как единое целое (переходы между связанными состояниями) или распасться на несвязанные части (переходы из связанных состояний в несвязанные). Примерами последних служат фотодиссоциация, фотоионизация и др. фотохим. р-ции (см. Фотохимия).
Безызлучательные К. п. происходят между нестационарными состояниями квантовой системы. В зависимости от того, между какими степенями свободы мол. системы осуществляется перенос энергии, возможны электронно-колебат., колебательно-колебат., колебательно-вращат. и т. п. безызлучат. К. п., а также переходы, соответствующие переносу энергии от внутримол. степеней свободы к тепловому движению. С безызлучат. К. п. обычно можно связать относительно резкое изменение к.-л. св-ва системы. Так, предиссоциация молекул, к-рая является одним из безызлучат. К. п., связана с переносом энергии от электронной подсистемы к ядерной и м. б. охарактеризована изменением межъядерного расстояния. Изменение спинового состояния квантовой системы характерно для интеркомбинац. конверсии, к-рая является одним из К. п., идущих с изменением мультиплетности состояния. Изменение момента кол-ва движения равновесной ядерной конфигурации характерно для процессов колебательно-вращат. релаксации. В твердых телах безызлучат. К. п. могут происходить из-за переноса энергии между разл. типами квазичастичных возбуждений - экситонами, фононами и т. д.
Безызлучат. К. п. часто качественно характеризуют временем релаксации, равным времени, за к-рое происходит передача энергии в системе. Для атомов, молекул и т.п., находящихся в возбужденных состояниях, всегда существует конкуренция между неск. возможностями для К. п., как безызлучательных, так и излучательных. Разные типы электронных К. п. для молекулы типичного орг. соед. показаны на диаграмме (см. рис.), предложенной А. Яблоньским (1935).
Широкий класс безызлучат. К. п. составляют туннельные переходы частиц. Туннельные К. п. позволяют описать
р-ции в хим. и биол. системах, связанные с туннельным переносом электрона, а также расщепление энергетич. состояний в нежестких молекулах с неск. эквивалентными равновесными ядерными конфигурациями. Туннелированием
Квантовые переходы между электронными состояниями молекулы: основным синглетным (S0), первым возбужденным синглетным (S1) и низшим триплетным (T1). Прямыми линиями показаны поглощение (А) и излучательные переходы: Б-резонансная флуоресценция, Е-фосфоресценция. Ж-флуоресценция. Волнистые линии-безызлучательные переходы (B-колебат. релаксация, Г-внутр. конверсия, Д-интеркомбинац. конверсия).
, где -постоянная Планка, Dt - характерное время состояния. В уширение уровня вносят вклад как излучат., так и безызлучат. К. п. Если предположить, что ширина уровня DE мала по сравнению с энергией кванта излучения (v-частота), К. п. можно наглядно интерпретировать как переход между стационарными энергетич. состояниями системы.
Излучательные К. п. изучаются методами спектроскопии. Положение спектральной линии характеризует энергию перехода, а интенсивность и ширина линии - вероятность перехода. Совокупность всех параметров, определяющих взаимод. молекулы с излучением и связанных с интенсивностями спектральных линий, наз. радиац. характеристиками молекулы. В качестве радиац. характеристик
используются коэффициенты Эйнштейна, сила осциллятора, вероятности переходов (см. ниже).
Излучат. К. п. могут быть спонтанными и вынужденными. Спонтанное излучение (испускание) происходит независимо от внеш. воздействия на мол. систему. Вероятность спонтанного излучения, сопровождающегося испусканием квантов электромагн. энергии и переходом мол. системы с n-го энергетич. уровня на m-й, характеризуется коэф. Эйнштейна Апm - средним числом квантов, испускаемых системой за 1 с и отнесенных к числу молекул в системе. Вероятность поглощения и вынужденного испускания зависит от плотности электромагн. излучения и характеризуется коэф. Эйнштейна Вmn и Впт, равными соотв. числу квантов электромагн. поля, к-рое поглощается или вынужденно испускается системой в среднем в расчете на 1 молекулу за 1 с при единичной плотности излучения. Связь между коэф. Аnт, Втп, Вnm была получена А. Эйнштейном на основе термодинамич. рассмотрения и впоследствии строго обоснована в квантовой электродинамике. Она выражается соотношениями:
где gn(gт) - кратность вырождения энергетич. уровня n(m), с-скорость света. В мол. спектроскопии в качестве радиац. характеристики часто используется сила осциллятора fmn ~ vmnBmn. Коэф. Эйнштейна и силу осциллятора для мол. системы можно рассчитать, если известны волновые ф-ции исходных и конечных энергетич. состояний и оператор момента перехода
:
Роль оператора момента перехода
в наиб. типичных случаях играет оператор электрического дипольного момента.
Излучат. К. п. классифицируют по типам квантовых состояний, между к-рыми происходит переход. Электронные К. п. обусловлены изменением электронного распределения - переходами внеш. (валентных) электронов между орбиталями (типичные энергии DEnm ~ 2,6.105 Дж/моль, частоты излучения лежат в видимой и УФ областях спектра), ионизацией внутр. электронов (для элементов с зарядом ядра Z ~ 10 DЕпт ~ 1,3.108 Дж/моль, излучение в рентгеновском диапазоне), аннигиляцией электроннопозитронных пар (DЕnm ~ 1,3.1011 Дж/моль, излучение в g - диапазоне). При переходах из возбужденных электронных состояний в основное различают флуоресценцию (оба состояния, связанные К. п., имеют одинаковую мультиплетность) и фосфоресценцию (мультиплетность возбужденного состояния отличается от мультиплетности основного) (см. Люминесценция). Колебат. К. п. связаны с внутримол. процессами, сопровождающимися перестройкой ядерной подсистемы (DEmn ~ 1.103-5.104 Дж/моль, излучение в ИК диапазоне), вращат. К. п.-с изменением вращат. состояний молекул (10-10-2 см-1 ~ 1,2.102-1,2310-1 Дж/моль, излучение в микроволновой и радиочастотной областях спектра). Как правило, в мол. системах при электронных К. п. происходит изменение колебат. состояний, поэтому соответствующие К. п. наз. электронно-колебательными. Отдельно выделяют К. п., связанные с изменением ориентации спина электрона или атомных ядер (эти переходы оказываются возможными благодаря расщеплению энергетич. уровней системы в магн. поле), изменением ориентации квадрупольного электрич. момента ядер в электрич. поле. Об использовании указанных К. п. в хим. анализе и для изучения структуры молекул см. Вращательные спектры, Колебательные спектры, Электронные спектры. Мёссбауэровская спектроскопия, Электронный парамагнитный резонанс, Ядерный магнитный резонанс, Ядерный квадруполъный резонанс, Рентгеновская спектроскопия, Фотоэлектронная спектроскопия.
Помимо обычных одногвантовых переходов, в каждом из к-рых поглощается или испускается один квант энергии, возможны многофотонные процессы, представляющие собой либо последовательность неск. одноквантовых переходов, либо один К. п. системы между двумя квантовыми состояниями, но с излучением или поглощением неск. квантов одинаковой или разной энергии. Вероятность многоквантовых переходов быстро уменьшается с понижением интенсивности взаимодействующего с в-вом электромагн. излучения, поэтому их исследование стало возможным лишь благодаря применению лазеров. Простейший двухквантовый процесс - комбинац. рассеяние света, при к-ром частица (атом, молекула) одновременно поглощает квант энергии и испускает квант меньшей или большей энергии. При последоват. поглощении молекулой двух квантов света возможны в ряде случаев фотохим. р-ции (см. Двухквантовые реакции). Четырехквантовый переход является, напр., основой метода когерентного антистоксова рассеяния света (КАРС) (см. Комбинационного рассеяния спектроскопия). С помощью этого метода удается изучать такие состояния, переходы в к-рые запрещены при одноквантовых переходах.
Приближенная трактовка излучат. К. п. как переходов между стационарными состояниями системы справедлива только в случае взаимод. квантовых систем со слабым электромагн. полем. В сильных полях само понятие "уровень энергии квантовой системы" не м. б. определено. Для сильных периодич. полей вводится концепция ква-зиэнергетич. состояний, в рамках к-рой можно описывать изменения, происходящие с системой при взаимод. с полем.
Если квантовая система состоит из большого числа одинаковых подсистем, возможна синхронизация излучат. К. п. в разл. подсистемах, приводящая к возникновению когерентного излучения. Данное явление лежит в основе работы лазеров и др. квантовых генераторов излучения.
В результате излучат. К. п. система может остаться существовать как единое целое (переходы между связанными состояниями) или распасться на несвязанные части (переходы из связанных состояний в несвязанные). Примерами последних служат фотодиссоциация, фотоионизация и др. фотохим. р-ции (см. Фотохимия).
Безызлучательные К. п. происходят между нестационарными состояниями квантовой системы. В зависимости от того, между какими степенями свободы мол. системы осуществляется перенос энергии, возможны электронно-колебат., колебательно-колебат., колебательно-вращат. и т. п. безызлучат. К. п., а также переходы, соответствующие переносу энергии от внутримол. степеней свободы к тепловому движению. С безызлучат. К. п. обычно можно связать относительно резкое изменение к.-л. св-ва системы. Так, предиссоциация молекул, к-рая является одним из безызлучат. К. п., связана с переносом энергии от электронной подсистемы к ядерной и м. б. охарактеризована изменением межъядерного расстояния. Изменение спинового состояния квантовой системы характерно для интеркомбинац. конверсии, к-рая является одним из К. п., идущих с изменением мультиплетности состояния. Изменение момента кол-ва движения равновесной ядерной конфигурации характерно для процессов колебательно-вращат. релаксации. В твердых телах безызлучат. К. п. могут происходить из-за переноса энергии между разл. типами квазичастичных возбуждений - экситонами, фононами и т. д.
Безызлучат. К. п. часто качественно характеризуют временем релаксации, равным времени, за к-рое происходит передача энергии в системе. Для атомов, молекул и т.п., находящихся в возбужденных состояниях, всегда существует конкуренция между неск. возможностями для К. п., как безызлучательных, так и излучательных. Разные типы электронных К. п. для молекулы типичного орг. соед. показаны на диаграмме (см. рис.), предложенной А. Яблоньским (1935).
Широкий класс безызлучат. К. п. составляют туннельные переходы частиц. Туннельные К. п. позволяют описать
р-ции в хим. и биол. системах, связанные с туннельным переносом электрона, а также расщепление энергетич. состояний в нежестких молекулах с неск. эквивалентными равновесными ядерными конфигурациями. Туннелированием
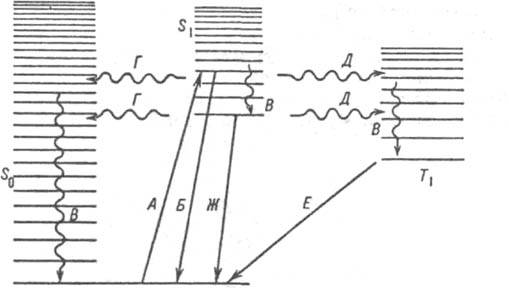
Квантовые переходы между электронными состояниями молекулы: основным синглетным (S0), первым возбужденным синглетным (S1) и низшим триплетным (T1). Прямыми линиями показаны поглощение (А) и излучательные переходы: Б-резонансная флуоресценция, Е-фосфоресценция. Ж-флуоресценция. Волнистые линии-безызлучательные переходы (B-колебат. релаксация, Г-внутр. конверсия, Д-интеркомбинац. конверсия).
частиц между конфигурациями ядер, отвечающими правым и левым изомерам, объясняется рацемизация оптич. изомеров. Механизмы хим. р-ции в твердых телах при низкой т-ре связаны с туннельным переносом тяжелых частиц. Правила отбора устанавливают, какие из К. п. (как излучательных, так и безызлучательных) возможны (являются разрешенными), а какие запрещены. Они исходят из наиб. общих соображений о симметрии пространства - времени и о симметрии индивидуальной мол. системы. Каждое из правил отбора связано с одним из законов сохранения. Различают строгие правила отбора, связанные, напр., с сохранением при К. п. полной энергии системы или полного момента кол-ва движения и проекции полного момента на одну из координатных осей, и приближенные правила отбора. Последние возникают в результате введения дополнительных (приближенных) законов сохранения, обусловленных наличием к.-л. малых взаимод., напр. спин-орбитального взаимодействия. В нерелятивистском приближении электронный спин системы является сохраняющейся величиной, и, как следствие, разрешенными м. б. только электронные К. п. без изменения спина. Однако в силу приближенного характера данного правила вероятность К. п. с изменением спина (интеркомбинац. конверсия) отлична от нуля и м. б. при определенных условиях достаточно велика. Для молекул типичные правила отбора связаны с изменением моментов кол-ва движения (полных электронных, полных спиновых, орбитальных электронных и других), проекций моментов кол-ва движения, с возможными изменениями типов симметрии относительно групп симметрии молекул (точечных, групп перестановок, групп симметрии нежестких молекул). Детальные сведения о правилах отбора для конкретных типов К. п. приведены в статьях о соответствующих мол. спектрах. Лит.: Берестецкий В. Б., Лифшиц Е. М., Питаевский Л. П., Квантовая электродинамика, 2 изд., М., 1980; Медведев Э. С., Оше-ров В. И., Теория безызлучательных переходов в многоатомных молекулах, М.. 1983; Гольданский В. И.. Трах тенберг Л. И., Флервв В. Н., Туннельные явления в химической физике, М., 1986. Б. И. Жимшский.