КВАДРУПОЛЬНЫЙ МОМЕНТ электрический, тензор Q, характеризующий электростатич. потенциал j(R) системы зарядов (атома, молекулы, кристалла) на большом расстоянии R от нее (по сравнению с размерами системы). Простейшая модель системы с К. м. - квадруполь, представляет собой два диполя с равными по величине, но противоположно направленными дипольными моментами. Если система зарядов электрически нейтральна и ее дипольный момент равен нулю, К. м. не зависит от выбора начала системы координат, в к-рой рассматриваются заряды.
К. м. Q появляется в третьем члене разложения j(R) в ряд по обратным степеням расстояния от начала системы координат, связанной с системой зарядов, до точки, определяемой концом вектора R. Это разложение для системы частиц с зарядами qi и радиусами-векторами ri (i-номер частицы) имеет вид:
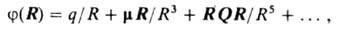где 
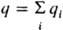- полный заряд системы, 
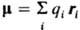-дипольный
момент системы, Q-K. м., компоненты к-рого Qab равны:
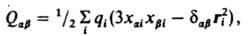xai и xbi - декартовы координаты вектора ri, т.е. x1i=xi, x2i=yi x3i=zi; dab принимает значение 1 при a=b и 0 при a№b (a,b=1,2,3).
Для системы с непрерывным распределением заряда с плотностью r(r) заряд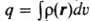 
(dv - элемент объема), дипольный момент m=
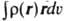, компоненты тензора К. м. равны:
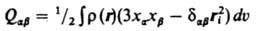Размерность К. м. в СИ-Кл.м2. Для молекул часто используют в качестве единиц К. м. величину 10-26 единиц заряда СГС.см2 ~ 3,3.10-40 Кл.м2; для К. м. ядер - величину 10-34 единиц заряда СГС.см2. Часто К. м. ядер выражают в единицах абс. заряда электрона е: Q/e=10-24см2, что соответствует ~ 4,803.10-34 единиц заряда СГС.см2.
К. м. для сферически симметричного распределения заряда (а также для распределений кубич. и тетраэдрич. симметрии) равен нулю, тогда как для систем с более низкой симметрией распределения заряда К. м., как правило, отличен от нуля. Поэтому К. м. есть характеристика распределения заряда в системах заряженных частиц. При этом всегда Qxx+Qyy+Qzz=0, а система координат м. б. выбрана так, что Qab=0 при a№b.
Во внеш. электрич. поле напряженности Е(Еx, Еу, Еz) энергия Е электрически нейтральной системы зарядов при m=0 равна:
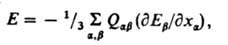причем производные РEb/Рxa предполагаются постоянными в области распределения зарядов.
В химии рассматривают квадрупольное взаимод. атомов, молекул на сравнительно больших расстояниях. Энергия такого взаимод. для частиц, не обладающих дипольным моментом, убывает с увеличением расстояния R пропорционально 1/R5 (см. Поляризуемость). К. м. молекул м. б. определены экспериментально (напр., по компонентам мол. g-фактора, по главным моментам инерции и анизотропии магн. восприимчивости, по величинам двойного лучепреломления при наличии градиента электрич. поля), а также м. б. рассчитаны методами квантовой механики. Так, для молекулы фторацетилена 
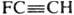Qzz=3,96, Qxx=Qyy=-1,98.10-26 единиц заряда СГС.см2 (ось z совпадает с осью молекулы), для молекулы СО Qzz=-4,3, Qxx-Qyy=2,15.10-26 (в тех же единицах).
К. м. обладают мн. атомные ядра. Если ядро с равномерно распределенным зарядом вытянуто вдоль нек-рой оси 2, Q>0; если ядро сплюснуто, то Q<0. К. м. ядер изменяются в широких пределах, напр. в единицах 10-24 см2 для ядер 17O Q=-0,021, 35С1 Q=-0,0789, 27Аl Q=0,149. Как правило, большие К. м. ядер положительны, т. е. распределение заряда в них соответствует вытянутому эллипсоиду вращения.
Взаимодействие К. м. ядра с электрич. полем кристалла или молекулы приводит к появлению различных по энергии состояний ядра, соответствующих разл. ориентации ядерного спина относительно осей симметрии кристалла или молекулы. Число разрешенных ядерных ориентации определяется ядерным магн. моментом, связанным со спином ядра, и равно 2I+1, где I - спиновое квантовое число ядра (см. Ядро атомное). Низший по энергии уровень отвечает такой ориентации ядра, при к-рой положит. заряд на сплюснутом или вытянутом ядре располагается ближе всего к наиб. плотности отрицат. заряда в электронном окружении этого ядра. Резонансное поглощение энергии
электромагн. поля, обусловленное квантовыми переходами между уровнями энергии, связанными с ядерными ориентациями, наз. ядерным квадруполышм резонансом.
Лит.: Гречишкин B.C., Ядерные квадрупольные взаимодействия в твердых телах, М., 1973; Флайгер У., Строение и динамики молекул, пер. с англ., т. 1-2, М., 1982. См. также лит. при ст. Ядерный квадрутмьпый резонанс. И. Ф. Степанов.
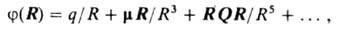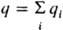где - полный заряд системы, 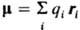-дипольный
момент системы, Q-K. м., компоненты к-рого Qab равны:
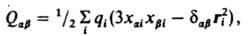xai и xbi - декартовы координаты вектора ri, т.е. x1i=xi, x2i=yi x3i=zi; dab принимает значение 1 при a=b и 0 при a№b (a,b=1,2,3).
Для системы с непрерывным распределением заряда с плотностью r(r) заряд 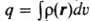(dv - элемент объема), дипольный момент m=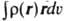, компоненты тензора К. м. равны:
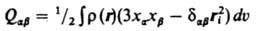Размерность К. м. в СИ-Кл.м2. Для молекул часто используют в качестве единиц К. м. величину 10-26 единиц заряда СГС.см2 ~ 3,3.10-40 Кл.м2; для К. м. ядер - величину 10-34 единиц заряда СГС.см2. Часто К. м. ядер выражают в единицах абс. заряда электрона е: Q/e=10-24см2, что соответствует ~ 4,803.10-34 единиц заряда СГС.см2.
К. м. для сферически симметричного распределения заряда (а также для распределений кубич. и тетраэдрич. симметрии) равен нулю, тогда как для систем с более низкой симметрией распределения заряда К. м., как правило, отличен от нуля. Поэтому К. м. есть характеристика распределения заряда в системах заряженных частиц. При этом всегда Qxx+Qyy+Qzz=0, а система координат м. б. выбрана так, что Qab=0 при a№b.
Во внеш. электрич. поле напряженности Е(Еx, Еу, Еz) энергия Е электрически нейтральной системы зарядов при m=0 равна:
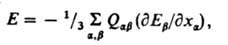причем производные РEb/Рxa предполагаются постоянными в области распределения зарядов.
В химии рассматривают квадрупольное взаимод. атомов, молекул на сравнительно больших расстояниях. Энергия такого взаимод. для частиц, не обладающих дипольным моментом, убывает с увеличением расстояния R пропорционально 1/R5 (см. Поляризуемость). К. м. молекул м. б. определены экспериментально (напр., по компонентам мол. g-фактора, по главным моментам инерции и анизотропии магн. восприимчивости, по величинам двойного лучепреломления при наличии градиента электрич. поля), а также м. б. рассчитаны методами квантовой механики. 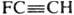Так, для молекулы фторацетилена Qzz=3,96, Qxx=Qyy=-1,98.10-26 единиц заряда СГС.см2 (ось z совпадает с осью молекулы), для молекулы СО Qzz=-4,3, Qxx-Qyy=2,15.10-26 (в тех же единицах).
К. м. обладают мн. атомные ядра. Если ядро с равномерно распределенным зарядом вытянуто вдоль нек-рой оси 2, Q>0; если ядро сплюснуто, то Q<0. К. м. ядер изменяются в широких пределах, напр. в единицах 10-24 см2 для ядер 17O Q=-0,021, 35С1 Q=-0,0789, 27Аl Q=0,149. Как правило, большие К. м. ядер положительны, т. е. распределение заряда в них соответствует вытянутому эллипсоиду вращения.
Взаимодействие К. м. ядра с электрич. полем кристалла или молекулы приводит к появлению различных по энергии состояний ядра, соответствующих разл. ориентации ядерного спина относительно осей симметрии кристалла или молекулы. Число разрешенных ядерных ориентации определяется ядерным магн. моментом, связанным со спином ядра, и равно 2I+1, где I - спиновое квантовое число ядра (см. Ядро атомное). Низший по энергии уровень отвечает такой ориентации ядра, при к-рой положит. заряд на сплюснутом или вытянутом ядре располагается ближе всего к наиб. плотности отрицат. заряда в электронном окружении этого ядра. Резонансное поглощение энергии
электромагн. поля, обусловленное квантовыми переходами между уровнями энергии, связанными с ядерными ориентациями, наз. ядерным квадруполышм резонансом.
Лит.: Гречишкин B.C., Ядерные квадрупольные взаимодействия в твердых телах, М., 1973; Флайгер У., Строение и динамики молекул, пер. с англ., т. 1-2, М., 1982. См. также лит. при ст. Ядерный квадрутмьпый резонанс. И. Ф. Степанов.