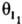Каталитических реакций кинетика

А₁ и А₂ из объемной фазы (газовой или жидкой), в-ва I₁ и I₂ из поверхностного слоя, занимающие на пов-сти доли и 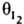соотв., то скорость р-ции

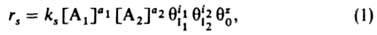
где k_s - константа скорости, [A₁] и [А₂] - концентрации А₁ и А₂; a₁, а₂, i₁, i₂ - числа молекул в-в, участвующих в р-ции; q₀-доля своб. пов-сти (или, при р-ции в р-ре, доля пов-сти, занятой р-рителем); z - число своб. мест пов-сти, к-рые требуются в дополнение к (i₁+i₂) местам, занятым молекулами I₁ и I₂, для образования активир. комплекса, т.е. переходного состояния (при гетерог. р-ции активир. комплекс подобен адсорбир. молекуле, однако может занимать на пов-сти более одного места). Фактически в р-ции не участвует более 3 частиц, так что те или иные сомножители в (1) всегда отсутствуют. Если отсутствуют 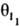, 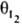и q₀, кинетич. ур-ние (1) определяет скорость гомог. р-ции, если эти сомножители присутствуют, - скорость гетерог. р-ции. Ур-ние для r_s, содержащее только величины q, иногда наз. законом действующих поверхностей. Ур-ние (1) описывает также процессы адсорбции и десорбции: если адсорбируется в-во A, z = 1 и r_s = k_s [A]q₀; если А десорбируется, z = 0 и r_-s=k_-sq_А (индексом — s обозначают величины, относящиеся к элементарной р-ции, обратной по отношению к р-ции номер s). В случае неидеальных систем правая часть (1) содержит дополнительно т. наз. кинетич. фактор активности, равный произведению коэф. активности вступающих в р-цию в-в, деленному на коэф. активности активир. комплекса. Зависимость от т-ры констант скорости элементарных р-ций описывается Аррениуса уравнением; предэкспоненц. фактор этого ур-ния м. б. вычислен или приближенно оценен как для гомогенных, так и для гетерогенно-каталитич. р-ций с помощью активированного комплекса теории. Скорость каталитич. р-ций в идеальной системе вычисляют на основе найденных по ур-нию (1) скоростей составляющих ее элементарных р-ций (см. Сложные реакции). В пром. реакторах каталитич. р-ции почти всегда стационарны или квазистационарны (см. Квазистационарности приближение). Скорость гетерогенно-каталитич. р-ции относят к единице площади пов-сти катализатора. Для техн. целей ее рассчитывают на единицу массы катализатора или на единицу объема слоя зерен катализатора (см. Активность катализатора). Часто итог каталитич. р-ции выражается двумя или более хим. ур-ниями. В таких случаях для расчета скорости образования целевого продукта важна селективность катализатора. В данной статье К. р. к. рассматривается в предположении, что р-ция происходит в кинетич. области, т. е. на ее скорость не влияют процессы переноса в-ва и тепла. Учет этих процессов, существенно влияющих на скорость мн. гетерогенно-каталитич. р-ций, рассматривается в ст. Макрокинетика. Сопоставление кинетич. ур-ний с опытными данными выполняют по-разному в зависимости от типа реактора. При использовании загрузочного реактора периодич. действия, являющегося замкнутой системой, кинетич. ур-ние интегрируют по времени, обычно используя приближение квазистационарности. В проточном трубообразном реакторе осуществляется стационарная р-ция; кинетич. ур-ние интегрируют по объему слоя катализатора, обычно в приближении режима идеального вытеснения, т. е. предполагая, что скорость движения объемной фазы одинакова по всему сечению реактора и можно пренебречь продольной диффузией. Надобность в интегрировании и в указанных упрощающих предположениях отпадает при использовании безградиентных реакторов, позволяющих измерять непосредственно скорость р-ции при данных концентрациях реагентов и продуктов.
Гомогенный катализ. Гетерогенный катализ на однородных поверхностях. Наиб. просты каталитич. р-ции, состоящие из двух стадий:

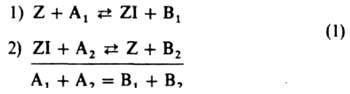
Здесь Z в случае гомог. катализа - молекула катализатора, в случае гетерог. катализа - место на пов-сти катализатора (адсорбц. центр), A₁ и А₂ - исходные в-ва, B₁ и В₂ - продукты р-ции, I - промежут. частица. Стрелками обозначены элементарные р-ции; в итоговом ур-нии ставится знак равенства. Скорости элементарных р-ций выражаются равенствами:

r₁=k_l[Z][A₁]; r_-1=k_-1[ZI][B₁];
r₂ = k₂[ZI][A₂];r_-2 = k_-2[Z][B₂] (2)

Кроме того, имеется уравнение баланса:

[Z] + [ZI] = [Z]_S, (3)

где [Z]_S в случае гомог. катализа - суммарная (определяемая аналит. методами) концентрация катализатора. В случае гетерог. катализа [ZI] и [Z] в (2) обозначают q₁ и q₀ и ур-нию (3) соответствует равенство: q₁+q₀=1, так что [Z]_S=1. При этом пропорциональность скорости р-ции числу мест на пов-сти учтена в значениях констант k₁, k_-1, и т. д. Для р-ций с участием газов принято вместо [A₁], [А₂] вводить в ур-ния типа (2) парциальные давления 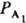,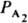. Если принять, что р-ция, протекающая по схеме (1), стационарна, то для ее скорости можно записать:

r = r₁-r_-l= r₂-r_-2. (4)

Ур-ния (2)-(4) дают:

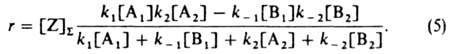
В частных случаях в схеме (1) B₁ или А₂ (либо оба эти в-ва) могут отсутствовать. Если отсутствует B₁ (при этом I совпадает с А₁) принимают B₁=1 и т. п. Возможно также, что вместо А₁ будут два в-ва - А'₁ и A''₁; тогда полагают [A₁]=[A'₁][А''₁] и т. п. Так, схема (1) отражает простейший механизм ферментативного катализа:

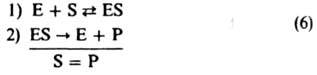
где Е-фермент, S-субстрат, Р-продукт. Предполагая р-цию в замкнутой системе квазистационарной и применяя равенство (5), получаем ур-ние Михаэлиса (1913):

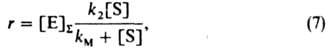
где k_M = (k_-1+k₂)/k_{-T. наз. константа Михаэлиса. Ур-ние (7) описывает кинетику мн. ферментативных р-ций. Пример гетерогенно-каталитич. р-ции с простым двустадийным механизмом - конверсия СО водяным паром на среднетемпературном (ок. 400 °С) катализаторе, гл. составной частью к-рого является Fe₃O₄:

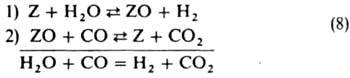
В (8) Z обозначает кислородную вакансию на пов-сти Fe₃O₄, к-рая образуется, когда молекула СО, ударяясь о пов-сть, удаляет с нее атом О (стадия 2). Вакансия вновь заполняется атомом О из Н₂О (стадия 1). В схеме (8) стадии пронумерованы так, чтобы она согласовалась с механизмом (1); при стационарной р-ции нумерация стадий произвольна, т. к. все элементарные р-ции происходят одновременно. Кислородные вакансии составляют лишь малую долю пов-сти, т. е. q₀ >> q₀; тогда из (2) и (4) следует:

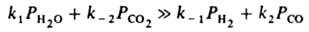
Предполагая поверхностный слой идеальным, получаем из (5):

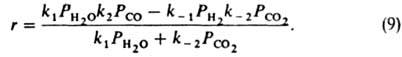
При равновесии (r= 0)

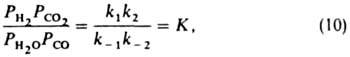
где К -константа равновесия. Отсюда ур-ние (9) можно представить в след, форме:

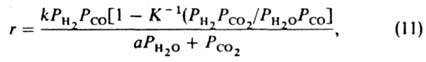
где k = k₁k₂/k_-2 и а=k_l/k_-2.

Если при стационарно протекающей по схеме (1) р-ции изменить скачком концентрации в-в в объемной фазе, а затем поддерживать их постоянными, то ZI и Z будут постепенно приближаться к значениям, соответствующим новому стационарному состоянию; при этом скорость р-ции будет изменяться по ур-нию:

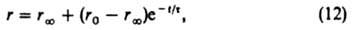
где t-время от момента изменения условии р-ции, r_: - новая стационарная скорость р-ции (достигаемая формально при t=:), r₀-скорость р-ции немедленно после изменения ее условий, t - постоянная, наз. временем релаксации скорости р-ции:

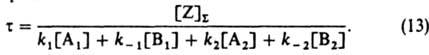
В случае гетерог. катализа вместо [Z]_S надо ввести в (13) L - число мест на единице площади пов-сти (-); при этом скорости элементарных р-ций должны быть определены как число актов р-ции на единице площади пов-сти за единицу времени. На основе (13) можно показать, что t [ 25u, где u=[Z]_S/r_: (при гомог. катализе) или u=L/r_: (при гетерог. катализе); u наз. временем оборота катализатора. При этом предполагается, что изменение скорости р-ции вызвано лишь изменением концентрации промежут. в-в, т. е. релаксация скорости р-ции является "собственной". При гетерогенно-каталитич. р-циях возможны также "сторонние" процессы релаксации скорости р-ции, вызванные обратимым изменением катализатора из-за изменения объемной фазы, к-рое приводит к изменению констант скорости элементарных р-ций. Напр., при окислении этилена в этилен-оксид кислородом на серебре сторонний релаксац. процесс обусловлен обратимым поглощением кислорода серебром. Он значительно медленнее собственного релаксац. процесса. В случае р-ций с механизмом более сложным, чем выражаемый схемой (1), в отсутствие сторонних релаксац. процессов, как правило, т не превышает и. Известны также автоколебат. р-ции, у к-рых стационарная скорость вовсе не устанавливается. В идеальных системах это возможно лишь при условии, что механизм р-ции содержит стадию взаимод. разл. промежут. в-в друг с другом (считая промежут. в-вами также своб. места пов-сти); тогда становится возможным существование более одного стационарного состояния (см. Колебательные реакции). Катализ на неоднородных поверхностях. Модель идеального адсорбир. слоя, как наиболее простая, широко применяется для описания кинетики гетерогенно-каталитич. р-ций. Она, однако, не всегда способна описать количественно явления на пов-стях реальных катализаторов. Напр., скорость адсорбции не пропорциональна q₀, а зависит от нее экспоненциально. В таких случаях необходимо отказаться по крайней мере от одного из предположений модели идеального адсорбир. слоя: либо считать места пов-сти неодинаковыми (т. наз. биографич. неоднородность), либо принять возможность взаимного влияния адсорбир. частиц (индуцир. неоднородность пов-сти). Тогда термин "однородная поверхность" будет означать почти то же, что и "идеальный адсорбир. слой", однако допускается возможность адсорбции частицы на двух и более соседних местах пов-сти. Согласно модели биографически неоднородной пов-сти, равновесие адсорбции в-ва I на однородной пов-сти (обозначается Z+I=ZI) подчиняется закону действующих масс:

(q₁/q₀P₁)=K_a (14)

Т. к. q₀+q₁=1, ур-ние (14) дает гиперболич. изотерму адсорбции Ленгмюра (см. Адсорбция). Константу адсорбц. равновесия К_а наз. адсорбц. коэффициентом. Для места биографически неоднородной пов-сти роль q₁ играет вероятность а того, что это место занято частицей I. Неоднородность пов-сти м. б. описана с помощью величины x=-lnК_а, наз. показателем десорбируемости; чем 4 больше, тем молекула I легче десорбируется. Произведение j(x)dx, где j(x) - дифференц. ф-ция распределения мест пов-сти по показателю десорбируемости, есть число мест пов-сти единичной площади, для к-рых показатель десорбируемости в-ва I принимает значения в пределах от до x + dx. Пусть x₀ - наименьшее, x₁ - наиб. значение x на данной пов-сти, так что если x < x₀ или x > x₁, то j(x)=0. Для описания опытных фактов достаточны ф-ции распределения в интервале x₀ < x < x₁ двух видов:

j(x)=A (15)
(равномерная неоднородность),
j(x) =Aе^gx, 0<g<1 (16)

(экспоненциальная неоднородность), где А - постоянная, g=T/q, q - постоянная, имеющая размерность т-ры Т. Распределение (16) формально переходит в (15) при g=0. Можно также допустить, что -1<g<1. Для области средних покрытий, для к-рьгх при x=x₀ s@1, при x=x₁ s@0, распределение (15) приводит к логарифмич. изотерме адсорбции Темкина, а распределение (16) - к степенной изотерме Фрейндлиха. Гиперболич. изотерма Ленгмюра обычно не описывает адсорбц. равновесие на катализаторах. Связь константы равновесия К элементарной р-ции Z+A:ZI+B с ее константой скорости k определяется соотношением:

k=gK^a, 0<a<1, (17)

где g и a - постоянные, a не зависит от Т. Постоянную a часто наз. коэф. переноса, а (17)-правилом переноса. Соотношение, аналогичное (17), связывает также k с К_а, т. к. К пропорциональна К_а. Единичный акт элементарной р-ции сопровождается уменьшением на единицу числа своб. мест пов-сти. Для обратной р-ции, при к-рой место освобождается, коэф. переноса обозначают р. Из условий хим. равновесия следует, что для каждой стадии s a_s+b_s=1, g_s=g_-s Зависимости, аналогичные (17), установлены экспериментально Й. Брёнстедом для р-ций гомог. кислотно-основного катализа, М. Поляни и Н. Н. Семеновым - для серий сходных гомог. р-ций с участием атомов и своб. радикалов, А. Н. Фрумкиным - для электродных процессов; теоретич. интерпретация этих зависимостей дана М. Эвансом и М. Поляни. Чтобы получить кинетику р-ции (1) на неоднородной пов-сти, для упрощения принимают, что коэф. переноса стадий 1 и 2 одинаковы: a₁=a₂=a. Интегрирование вкладов разл. мест пов-сти в скорость р-ции дает:

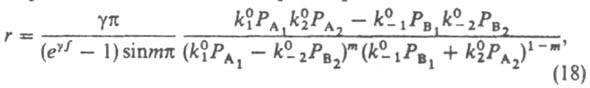
где m=a-g (0<m<1), f=x₁-x₀ - т наз. показатель неоднородности пов-сти, k⁰₁, k⁰₂, k⁰_-1, k⁰_-2 - значения соотв. констант скорости при x=0. Если g=0 (равномерная неоднородность), то g/(е^gf-1) заменяется на 1/f, а m - на a. В области малых покрытий (у всех мест s<<1) скорость р-ции, протекающей по схеме (1), описывается ур-нием (18) с m=0; для области больших покрытий, в к-рой у всех мест s@1, - ур-нием (18) с m=1. В обоих случаях выражение для r по форме не отличается от получаемого из (5), различны лишь значения постоянных. Этим объясняется то, что ур-ние (9) согласуется с опытными данными, хотя, как показывает исследование равновесия стадии 1 схемы (8), пов-сть катализатора при снятии кислорода равномерно неоднородна. В качестве примера р-ции на неоднородной пов-сти в области средних покрытий рассмотрим синтез NH₃. Если парциальное давление NH₃ не слишком мало, адсорбция азота является стадией, определяющей скорость процесса, и механизм р-ции м. б. представлен схемой:

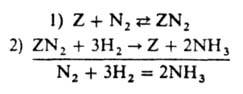
равновесная стадия 2 в действительности состоит из стадий гидрирования адсорбир. азота, но это не существенно для вывода кинетич. ур-ния, т. к. равновесие не зависит от механизма, по к-рому устанавливается. Р-ция происходит при средних покрытиях пов-сти азотом и малых покрытиях водородом и промежут. продуктами гидрирования, поэтому применимо ур-ние (18). Квазиравновесность стадии 2 означает, что k⁰_-2>>k⁰₁P_A1; k⁰₂P_A2>>k⁰_-1P_B1. T. к. P_A1=P_N2, P_A2=P³_H2, Р_В1=1, Р_B2=P²_NH3, получаем:

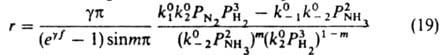
или

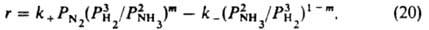
где k₊ и k_- - постоянные. При равновесии r=0, следовательно, k₊/k_-=К, где К - константа равновесия р-ции N₂ + ЗН₂ = 2NH₃. Она не зависит от характеристик катализатора, поэтому ур-ние (20) содержит лишь 2 постоянные, т и k₊ (или k_-), подлежащие определению из результатов измерений скорости р-ции. Для промотированных железных кат., применяемых в пром-сти, обычно получают m = 0,5; при этом a=0,5 и g=0. Ур-ние (20) подтверждено опытами при давлениях от 0,025 до 50 МПа. При более высоких давлениях требуется ввести поправку, учитывающую отклонение газов от идеальности и влияние давления на константы скорости. Правило переноса (18) выполняется для данной элементарной р-ции не только при переходе от одного места неоднородной пов-сти к другому, но также (хотя и более грубо) при переходе от одного катализатора к другому. Если к стадиям р-ции, происходящей по схеме (1) на разл. однородных пов-стях, применимо правило переноса (18), скорость р-ции максимальна на таком катализаторе, для к-рого 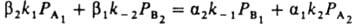. Следовательно, при необратимости стадий и при g₁=g₂, a₁=a₂=0,5 и P_А1@P_A2 скорость р-ции максимальна, если стандартное изменение энергии Гиббса в первой стадии DG⁰₁ примерно равно половине стандартного изменения энергии Гиббса для р-ции в целом. Сходное утверждение, но относящееся к тепловым эффектам стадий и р-ции в целом, наз. принципом энергетич. соответствия (впервые сформулирован А. А. Баландиным). Лит.. Уолтер Ч., Кинетика ферментативных реакций, пер. с англ., М., 1969; Снаговский Ю. С., Островский Г М., Моделирование кинетики гетерогенных каталитических процессов, М., 1976; Киперман С Л., Основы химической кинетики в гетерогенном катализе, М., 1979; Яблонский Г С., Быков В. И., Горбань А. Н., Кинетические модели каталитических реакций, Новосиб., 1983; Тёмкин М И., "Кинетика и катализ", 1984, т. 25. в. 2,с. 299 305; Temkin М. I., "Advances in Catalysis", 1979, v. 28, р. 173 281; Boudart M., Djegamariadassou G.. Cinetique des reactions en catalyse heterogene, P., 1982. М.И. Тёмкин.