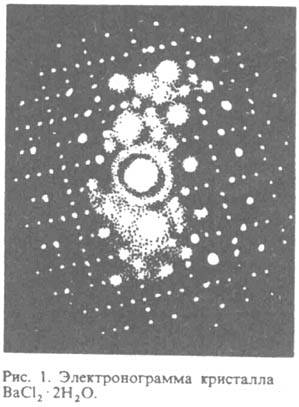
Поэтому различные Д. м. дают сведения, дополняющие друг друга.
Основы теории дифракции. Плоскую монохроматич. волну с длиной волны l и волновым вектором k0, где |k0| = 2p/l, можно рассматривать как пучок частиц с импульсом р, где |р| = h/l; h - постоянная Планка. Амплитуда F волны (с волновым вектором k), рассеянной совокупностью из п атомов, определяется ур-нием:
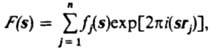
где вектор s = (k — k0)/2p, s = 2sinq/l, 2q - угол рассеяния, fj(s) - атомный фактор, или фактор атомного рассеяния, т. е. ф-ция, определяющая амплитуду рассеяния изолированным j-м атомом (или ионом); rj - его радиус-вектор. Аналогичное выражение можно записать, если считать, что объект объемом V обладает непрерывной рассеивающей плотностью r(r):
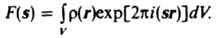
По такой же ф-ле рассчитывают и атомный фактор f(s); при этом r(r) описывает распределение рассеивающей плотности внутри атома. Значения атомного фактора специфичны для каждого вида излучения.
Рентгеновские лучи рассеиваются электронными оболочками атомов. Соответствующий атомный фактор fр при q = 0 численно равен числу электронов Z в атоме, если fр выражен в т. наз. электронных единицах, т. е. в относит. единицах амплитуды рассеяния рентгеновского излучения одним своб. электроном. С увеличением угла рассеяния fр уменьшается (рис. 2).
Рассеяние электронов определяется электростатич. потенциалом атома j(r) (r - расстояние от центра атома). Атомный фактор для электронов fэ связан с fр соотношением:
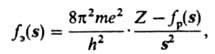
где е - заряд электрона, m - его масса. Абс. значения fэ (~10-8 см) значительно больше, чем fр (~10-11 см), т. е. атом рассеивает электроны сильнее, чем рентгеновские лучи; fэ уменьшается с ростом sinq/l более резко, чем fр, но зависимость fэ от Z слабее (рис. 3).
Нейтроны рассеиваются ядрами атомов (фактор fн), а также благодаря взаимодействию магн. моментов нейтронов с отличными от нуля магн. моментами атомов (фактор fнм). Радиус действия ядерных сил очень мал (~10-6 нм), поэтому величины fн практически не зависят от q. Кроме того, факторы fн не зависят монотонно от ат. н. Z и, в отличие от fр и fэ, могут принимать отрицат. значения.
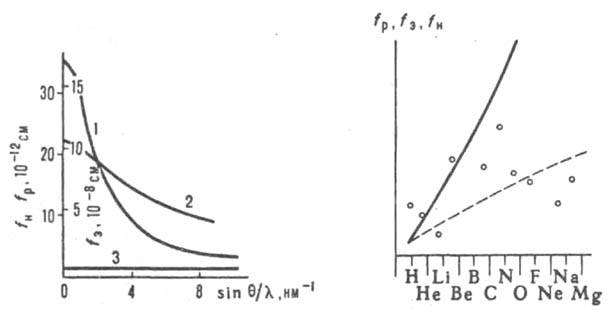
Рис. 2. Зависимость абсолютных значений атомных факторов рентгеновских лучей (1), электронов (2) и нейтронов (3) от угла рассеяния q (для Рb).
Рис. 3. Относительная зависимость усредненных по углу атомных факторов рентгеновских лучей (сплошная линия), электронов (штриховая) и нейтронов (кружки) от атомного номера Z.
По абс. величине fн~10-12 см. При точных расчетах рассматривают отклонения распределения электронной плотности или потенциала атомов от сферич. симметрии и т. наз. атомно-температурный фактор, учитывающий влияние тепловых колебаний атомов на рассеяние.
Для мёссбауэровского g-излучения помимо рассеяния на электронных оболочках атомов существ. роль может играть резонансное рассеяние на ядрах (напр., 57Fe), для к-рых наблюдается эффект Мёссбауэра, что и используется в структурном анализе. Фактор рассеяния fм зависит от волновых векторов и векторов поляризации падающей и рассеянной волн.
Интенсивность I(s) рассеяния объектом пропорциональна квадрату модуля амплитуды: I(s)~|F(s)|2. Экспериментально можно определить лишь модули |F(s)|, а для построения ф-ции рассеивающей плотности r(r) необходимо знать также фазы j(s) для каждого s. Тем не менее теория Д. м. позволяет по измеренным I(s) получить ф-цию r(r), т. е. определить структуру в-в. При этом лучшие результаты получают при исследовании кристаллов.
Структурный анализ кристаллов. Монокристалл представляет собой строго упорядоченную систему, поэтому при дифракции образуются лишь дискретные рассеянные пучки, для к-рых вектор рассеяния s равен т. наз. вектору обратной решетки Нhkl;
Нhkl = ha* + kb* + lс*,
где a* = [bс]/W, b* = [сa]/W, с* = [ab]/W; a,b и с - параметры ячейки кристалла; W - ее объем, W = (a[bс]). Распределение рассеивающей плотности в элементарной ячейке представляется в виде ряда Фурье:
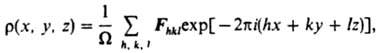
где h, k, l - т. наз. миллеровские индексы отражающей плоскости, Fhkl = |Fhkl|exp[ijhkl] - соответствующая структурная
амплитуда рассеянного излучения, jhkl - ее фаза. Для построения ф-ции r(х, у, z)по экспериментально определяемым величинам |Fhkl| применяют метод проб и ошибок, построение и анализ ф-ции межатомных расстояний, метод изоморфных замещений, прямые методы определения фаз (см. Рентгенография). Обработка эксперим. данных на ЭВМ позволяет восстанавливать структуру в виде карт распределения рассеивающей плотности (рис. 4).
Структуры кристаллов изучают гл. обр. с помощью рентгеновского структурного анализа. Этим методом определено более 100 тыс. структур неорг. и орг. кристаллов. Для неорг. кристаллов с применением разл. методов уточнения (учет поправок на поглощение, анизотропию атомно-температурного фактора и т. д.) удается восстановить ф-цию r(r) с разрешением до 0,05 нм и определять расстояния между атомами с точностью ~10-4 нм.
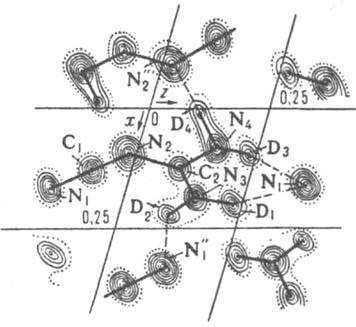
Рис. 4. Проекция ядерной плотности кристаллич. структуры дейтерированного дициандиамида C2N4D4. Пунктиром соединены атомы, связанные водородной связью.
Это позволяет определять анизотропию тепловых колебаний атомов, особенности распределения электронов, обусловленные хим. связью, и т. д. С помощью рентгеноструктурного анализа удается расшифровывать атомные структуры кристаллов белков, молекулы к-рых содержат тысячи атомов.
Дифракция рентгеновских лучей используется также для изучения дефектов в кристаллах (в рентгеновской топографии), исследования приповерхностных слоев (в рентгеновской спектрометрии), качеств. и количеств. определения фазового состава поликристаллич. материалов (в рентгеновском фазовом анализе) и др.
Электронография как метод изучения структуры кристаллов имеет след. особенности: 1) взаимод. в-ва с электронами намного сильнее, чем с рентгеновскими лучами, поэтому дифракция происходит в тонких слоях в-ва толщиной 1-100 нм; 2) fэ зависит от атомного номера слабее, чем fр, что позволяет проще определять положение легких атомов в присут. тяжелых; 3) благодаря тому что длина волны обычно используемых быстрых электронов с энергией 50-100 кэВ составляет ок. 5.10-3 нм, геом. интерпретация электронограмм существенно проще. Структурная электронография широко применяется для исследования тонкодисперсных объектов, а также для изучения разного рода текстур (глинистые минералы, пленки полупроводников и т. п.). Дифракция электронов низких энергий (10-300 эВ, l 0,1-0,4 нм) - эффективный метод исследования пов-стей кристаллов: расположения атомов, характера их тепловых колебаний и т. д. Электронная микроскопия восстанавливает изображение объекта по дифракц. картине и позволяет изучать структуру кристаллов с разрешением 0,2-0,5 нм.
Источниками нейтронов для структурного анализа служат ядерные реакторы на быстрых нейтронах, а также импульсные реакторы. Спектр пучка нейтронов, выходящих из канала реактора, непрерывен вследствие максвелловского распределения нейтронов по скоростям (его максимум при 100°С соответствует длине волны 0,13 нм). Монохроматизацию пучка осуществляют разными способами - с помощью кристаллов-монохроматоров и др. Нейтронография используется, как правило, для уточнения и дополнения рентгеноструктурных данных. Отсутствие монотонной зависимости
fи от атомного номера позволяет достаточно точно определять положение легких атомов. Кроме того, изотопы одного в того же элемента могут иметь сильно различающиеся значения fи (так, fи у водорода 3,74.10-13 см, у дейтерия 6,67.10-13 см). Это дает возможность изучать расположение изотопов и получать дополнит. сведения о структуре путем изотопного замещения (рис. 4). Исследование магн. взаимод. нейтронов с магн. моментами атомов дает информацию о спинах магн. атомов.
Мёссбауэровское g-излучение отличается чрезвычайно малой шириной линии - ок. 10-8 эВ (тогда как ширина линии характеристич. излучения рентгеновских трубок ок. 1 эВ). Это обусловливает высокую временную и пространств. согласованность резонансного ядерного рассеяния, что позволяет, в частности, изучать магн. поле и градиент электрич. поля на ядрах. Ограничения метода - слабая мощность мёссбауэровских источников и обязательное присутствие в исследуемом кристалле ядер, для к-рых наблюдается эффект Мёссбауэра.
Структурный анализ некристаллических веществ. Отдельные молекулы в газах, жидкостях и твердых аморфных телах по-разному ориентированы в пространстве, поэтому определить фазы рассеянных волн, как правило, невозможно. В этих случаях интенсивность рассеяния обычно представляют с помощью т. наз. межатомных векторов rjk, к-рые соединяют пары разл. атомов (j и k) в молекулах: rjk = rj - rk. Картина рассеяния усредняется по всем ориентациям:
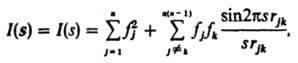
где rjk = |rj - rk|. В правой части ур-ния первая сумма представляет собой т. наз. атомную составляющую рассеяния Ia(s), вторая - мол. составляющую Iм(s). По мол. составляющей рассчитывают ряд важных характеристик молекул, напр. т. наз. ф-цию радиального распределения (спектр межъядерных расстояний), по к-рой строят геом. модель молекулы. Приведенное выражение для I(s) лежит в основе газовой электронографии - метода изучения строения своб. молекул в газе или паре.
Атомную структуру в-ва можно исследовать с помощью т. наз. EXAFS-метода (рентгеновской спектроскопии на краю поглощения), в к-ром исследуемое в-во облучают синхротронным излучением с длиной волны, соответствующей краю полосы поглощения к.-л. атома (или атомов) в структуре. Тогда по полученному спектру поглощения получают данные о расположении атомов в окрестности выбранного атома (атомов).
Для систем, обладающих цилиндрич. симметрией (напр., полимеры, жидкие кристаллы), картина рассеяния представляет собой совокупность более или менее размытых кольцевых областей - диффузных пятен, по к-рой удается сделать ряд заключений о структуре объекта. При изучении стекол, разл. порошков, сплавов, р-ров макромолекул анализ рассеяния вблизи первичного пучка (т. наз. малоугловое рассеяние) позволяет определять такие характеристики дисперсной фазы, как средние размеры пор, кластеров, их распределение по размерам. При исследовании разбавленных р-ров идентичных частиц, напр., в случае биополимеров, интенсивность малоуглового рассеяния пропорциональна усредненной по всем ориентациям интенсивности рассеяния одной частицей, что позволяет определять геом. параметры и массы исследуемых частиц.
Лит. Иверонова В. И., Ревкевич Г. П., Теория рассеяния рентгеновских лучей, М., 1972; Вилков Л. В., Мастрюков В. С., Садова Н. И., Определение геометрического строения свободных молекул, Л., 1978; Бландел Т., Джонсон Л., Кристаллография белка, пер. с англ., М., 1979;Нозиг Ю. 3., Озеров Р. П., Хенниг К., Нейтроны и твердое тело, т. 3, М., 1979; Современная кристаллография, под ред. Б. К. Вайнштейна, т. 1, М., 1979; Каули Дж., Физика дифракции, пер. с англ., М., 1979.
Б. К. Вайнштейн. Д. И. Свергун.


