ДИНАМИКА ЭЛЕМЕНТАРНОГО АКТА хим. реакции, изучает превращение отдельной молекулы или комплекса взаимодействующих молекул из заданного начального квантового состояния i в определенное конечное состояние f (от англ. initial и final соотв.). Для процессов в газовой фазе элементарные акты - гл. обр. столкновения молекул, сопровождающиеся передачей энергии, мономолекулярными превращениями или бимолекулярными р-циями; в конденсир. средах (жидкостях и твердых телах) элементарные акты взаимод. частиц рассматриваются с учетом взаимод. системы с окружающей средой. Теоретич. исследование элементарных актов основано на изучении методами классич. или квантовой механики особенностей движения (динамики) электронов и атомных ядер, составляющих систему частиц, к-рые участвуют в элементарном акте (одна молекула в случае мономолекулярных превращений, две - при бимолекулярных р-циях, три - при тримолекулярных).
Основные понятия и экспериментальные методы. Осн. параметр, рассматриваемый в Д. э. а., - вероятность перехода Pif , к-рая характеризует увеличение заселенности квантового состояния f продуктов в результате уменьшения заселенности состояния i реагентов в единицу времени. Необходимость введения такого параметра (вместо константы скорости процесса - хим. р-ции или неупругого соударения частиц) обусловлена тем, что Д. э. а. изучает мол. превращения на микроскопич. уровне и не рассматривает превращения всех частиц в единице объема, т. е. полные концентрации реагирующих в-в. В условиях, когда задание одного начального квантового состояния частицы (атома, молекулы) и определение одного конечного ее состояния невозможно по к.-л. причинам (напр., в связи с недостаточной разрешающей способностью эксперим. методики), Д. э. а. изучает превращение из группы состоянии, задаваемой средним квантовым числом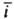
с разбросом значений 
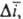в др. группу, заданную соотв. величинами 
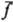и 
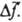Особенности движения электронов и ядер молекул, взаимодействующих при соударениях, определяются в осн. энергией относит. движения молекул, их ориентацией в пространстве и внутр. состоянием, задаваемым набором квантовых чисел (см. Столкновений теория). Соответственно и эксперим. исследования Д. э. а. основаны на использовании методов, к-рые позволяют оптимальным образом "приготовлять" реагенты и регистрировать продукты. В частности, молекулярных пучков метод обеспечивает заданную относит. энергию молекул реагентов; отклоняющие внеш. поля позволяют создавать предпочтит. ориентацию молекул относительно заданного направления (напр., вектора скорости); лазерное возбуждение - задавать определенное колебат. и вращат. состояния молекул. Для анализа состояний продуктов используется измерение дифференциальных сечений р-ций с дополнит. определением распределения частиц по скоростям; лазерно-индуцированная флуоресценция позволяет определять конечные колебат. и вращат. состояния (см. Люминесценция); используют также хемилюминесценцию в видимой и ИК областях спектра. Эксперим. результаты обычно формулируют в виде набора величин (напр., т. наз. детальных или поуровневых сечений), к-рые непосредственно связаны с вероятностями переходов
Рif .
Процессы в газовой фазе. Д. э. а. изучает столкновения молекул без учета послед. процессов (вторичных столкновений и др.) и внутримолекулярные изменения в изолир. молекуле. Обычно в качестве исходных данных, к-рыми оперирует теория, берут вычисленные методами квантовой химии или построенные эмпирически поверхности потенциальной энергии. Это позволяет устранить все сложные аспекты теории, связанные с учетом перестройки электронной конфигурации частиц, и свести задачу к изучению движения атомных ядер. Если выполняются условия адиабатического приближения, ядра (и связанные с ними окружающие их электронные оболочки) движутся под влиянием действующих между ними сил, к-рые определяются видом пов-сти потенц. энергии. Это движение описывается законами квантовой механики, но иногда возможно ограничиться законами классич. механики. Если условия адиабатич. приближения не выполняются, следует учитывать переходы между разл. пов-стями потенц. энергии. Вероятности таких переходов вычисляются только в рамках квантовомех. теории. В случае мономолекулярного процесса Д. э. а. изучает в осн. закономерности перераспределения энергии изолир. молекулы по степеням свободы. Практически важный аспект этого исследования - выяснение возможностей специфичности (т. е. направленности) мономолекулярного превращения при том или ином способе передачи заданной энергии реагирующей молекуле. Напр., если молекула возбуждается по одной из связей (в результате хим. активации или поглощения фотона), представляет интерес определить вероятность р-ций с участием др. связей. Одна из важных кинетич. характеристик, к-рая м. б. определена методами Д. э. а., - микроскопич. константа скорости (см. Мономолекулярные реакции). Задачи Д. э. а. бимолекулярных р-ций - выяснение того, какова роль энергии разл. степеней свободы молекул реагентов в преодолении потенц. барьера, разделяющего исходное и конечное состояния (см. Энергия активации), а также вычисление ф-ции распределения выделяющейся при р-ции энергии по степеням свободы частиц продуктов. Решение этих задач обеспечивает возможность стимулирования данной р-ции, напр., посредством предварит. возбуждения определенного рода колебаний в молекулах реагента лазерным излучением. Удается установить предпочтительную форму выделяющейся при р-ции энергии (поступат., колебат. или вращательную), что позволяет использовать тот или иной процесс для вторичного преобразования энергии (напр., для преобразования энергии хим. р-ции в энергию когерентного излучения лазера, см. Лазеры химические). Величины, к-рые характеризуют кинетику бимолекулярных процессов - неупругих столкновений или р-ций обмена, замещения, отрыва и т. п., - это детальные сечения р-ции или микроскопич. константы скорости (см. Бимолекулярные реакции). В ряде случаев полное динамич. описание элементарного акта взаимод. частиц в газовой фазе допускает заметное упрощение. Обычно это связано либо со спецификой динамич. поведения, проявляющейся в хаотич. характере движения системы, либо со спец. заданием начальных условий для системы, участвующей в элементарном акте. В первом случае возможен статистич. подход к описанию элементарного акта, для чего вполне достаточно весьма общей информации о св-вах системы (напр., знания плотности энергетич. состояний). Во втором случае, если начальные состояния частиц отвечают распределению Максвелла - Больцмана, расчет нек-рых кинетич. характеристик процесса м. б. проведен в рамках активированного комплекса теории.
Процессы в конденсированных средах. Д. э. а. изучает эволюцию рассматриваемой системы частиц в условиях ее непрерывного взаимод. с окружением. Поскольку исследование динамич. ур-ний системы и окружения слишком сложно и даже не точно определено (что есть окружение?), теоретич. описание таких процессов требует отказа от детерминированной картины механики. Чисто динамич. ур-ния заменяют стохастическими, в к-рых движение системы частиц (атомов, молекул) по пов-стям потенц. энергии дополняется учетом взаимод. системы с окружением, к-рое носит случайный (стохастический) характер из-за участия в нем большого числа частиц окружения. Мат. способ описания такого взаимод. - ф-ция корреляции случайной силы, действующей на систему со стороны окружения. Ф-ции м. б. независимо рассчитаны, напр., методами молекулярной динамики, использующими компьютерную симуляцию поведения большого числа частиц, или иногда определены экспериментально. В основе совр. теоретич. подхода лежит т. наз. обобщенное ур-ние Ланжевена, к-рое учитывает случайное действие окружения на выделенную систему частиц и обратную р-цию системы на окружение. При нек-рых упрощающих предположениях относительно взаимод. частиц внутри системы и взаимод. системы с окружением оказывается возможным построение целой иерархии приближений, к-рые формулируются в виде упрощающих ур-ний. К ним относятся ур-ние Фоккера - Планка (справедливо при условии, когда время "рассасывания" флуктуации в среде намного меньше характерных времен движения в системе), ур-ние Смолуховского (справедливо при том же предположении и при дополнит. условии установления почти равновесного распределения по скоростям частиц системы), диффузионное ур-ние Фика (справедливо при тех же предположениях и дополнит. условии своб. диффузии реагентов).
Химические реакция в сильных внешних полях - электрич., магн. и световых - сравнительно новое направление Д. э. а. В этих случаях наряду с взаимод. частиц между собой и с окружением приходится рассматривать их взаимод. с полями. Последние изменяют вероятности переходов; в частности, могут открываться новые пути превращений, к-рые в отсутствие полей запрещены. Возникает принципиальная возможность направленного влияния на элементарный акт воздействием внеш. излучения. Примером могут служить т. наз. радиационные столкновения, когда при сближении реагентов поглощается фотон, система переходит в новое электронное состояние, обладающее повышенной (и, возможно, направленной) реакц. способностью. Др. пример -влияние магн. полей на спиновые состояния частиц реагентов, от к-рых в решающей степени зависит эффективность элементарного акта (см. Магнитно-спиновые эффекты).
Основные понятия и экспериментальные методы. Осн. параметр, рассматриваемый в Д. э. а., - вероятность перехода Pif , к-рая характеризует увеличение заселенности квантового состояния f продуктов в результате уменьшения заселенности состояния i реагентов в единицу времени. Необходимость введения такого параметра (вместо константы скорости процесса - хим. р-ции или неупругого соударения частиц) обусловлена тем, что Д. э. а. изучает мол. превращения на микроскопич. уровне и не рассматривает превращения всех частиц в единице объема, т. е. полные концентрации реагирующих в-в. В условиях, когда задание одного начального квантового состояния частицы (атома, молекулы) и определение одного конечного ее состояния невозможно по к.-л. причинам (напр., в связи с недостаточной разрешающей способностью эксперим. методики), Д. э. а. изучает превращение из группы состоянии, задаваемой средним квантовым числом
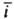с разбросом значений 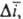в др. группу, заданную соотв. величинами 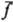и
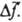Особенности движения электронов и ядер молекул, взаимодействующих при соударениях, определяются в осн. энергией относит. движения молекул, их ориентацией в пространстве и внутр. состоянием, задаваемым набором квантовых чисел (см. Столкновений теория). Соответственно и эксперим. исследования Д. э. а. основаны на использовании методов, к-рые позволяют оптимальным образом "приготовлять" реагенты и регистрировать продукты. В частности, молекулярных пучков метод обеспечивает заданную относит. энергию молекул реагентов; отклоняющие внеш. поля позволяют создавать предпочтит. ориентацию молекул относительно заданного направления (напр., вектора скорости); лазерное возбуждение - задавать определенное колебат. и вращат. состояния молекул. Для анализа состояний продуктов используется измерение дифференциальных сечений р-ций с дополнит. определением распределения частиц по скоростям; лазерно-индуцированная флуоресценция позволяет определять конечные колебат. и вращат. состояния (см. Люминесценция); используют также хемилюминесценцию в видимой и ИК областях спектра. Эксперим. результаты обычно формулируют в виде набора величин (напр., т. наз. детальных или поуровневых сечений), к-рые непосредственно связаны с вероятностями переходов
Рif . Процессы в газовой фазе. Д. э. а. изучает столкновения молекул без учета послед. процессов (вторичных столкновений и др.) и внутримолекулярные изменения в изолир. молекуле. Обычно в качестве исходных данных, к-рыми оперирует теория, берут вычисленные методами квантовой химии или построенные эмпирически поверхности потенциальной энергии. Это позволяет устранить все сложные аспекты теории, связанные с учетом перестройки электронной конфигурации частиц, и свести задачу к изучению движения атомных ядер. Если выполняются условия адиабатического приближения, ядра (и связанные с ними окружающие их электронные оболочки) движутся под влиянием действующих между ними сил, к-рые определяются видом пов-сти потенц. энергии. Это движение описывается законами квантовой механики, но иногда возможно ограничиться законами классич. механики. Если условия адиабатич. приближения не выполняются, следует учитывать переходы между разл. пов-стями потенц. энергии. Вероятности таких переходов вычисляются только в рамках квантовомех. теории. В случае мономолекулярного процесса Д. э. а. изучает в осн. закономерности перераспределения энергии изолир. молекулы по степеням свободы. Практически важный аспект этого исследования - выяснение возможностей специфичности (т. е. направленности) мономолекулярного превращения при том или ином способе передачи заданной энергии реагирующей молекуле. Напр., если молекула возбуждается по одной из связей (в результате хим. активации или поглощения фотона), представляет интерес определить вероятность р-ций с участием др. связей. Одна из важных кинетич. характеристик, к-рая м. б. определена методами Д. э. а., - микроскопич. константа скорости (см. Мономолекулярные реакции). Задачи Д. э. а. бимолекулярных р-ций - выяснение того, какова роль энергии разл. степеней свободы молекул реагентов в преодолении потенц. барьера, разделяющего исходное и конечное состояния (см. Энергия активации), а также вычисление ф-ции распределения выделяющейся при р-ции энергии по степеням свободы частиц продуктов. Решение этих задач обеспечивает возможность стимулирования данной р-ции, напр., посредством предварит. возбуждения определенного рода колебаний в молекулах реагента лазерным излучением. Удается установить предпочтительную форму выделяющейся при р-ции энергии (поступат., колебат. или вращательную), что позволяет использовать тот или иной процесс для вторичного преобразования энергии (напр., для преобразования энергии хим. р-ции в энергию когерентного излучения лазера, см. Лазеры химические). Величины, к-рые характеризуют кинетику бимолекулярных процессов - неупругих столкновений или р-ций обмена, замещения, отрыва и т. п., - это детальные сечения р-ции или микроскопич. константы скорости (см. Бимолекулярные реакции). В ряде случаев полное динамич. описание элементарного акта взаимод. частиц в газовой фазе допускает заметное упрощение. Обычно это связано либо со спецификой динамич. поведения, проявляющейся в хаотич. характере движения системы, либо со спец. заданием начальных условий для системы, участвующей в элементарном акте. В первом случае возможен статистич. подход к описанию элементарного акта, для чего вполне достаточно весьма общей информации о св-вах системы (напр., знания плотности энергетич. состояний). Во втором случае, если начальные состояния частиц отвечают распределению Максвелла - Больцмана, расчет нек-рых кинетич. характеристик процесса м. б. проведен в рамках активированного комплекса теории.
Процессы в конденсированных средах. Д. э. а. изучает эволюцию рассматриваемой системы частиц в условиях ее непрерывного взаимод. с окружением. Поскольку исследование динамич. ур-ний системы и окружения слишком сложно и даже не точно определено (что есть окружение?), теоретич. описание таких процессов требует отказа от детерминированной картины механики. Чисто динамич. ур-ния заменяют стохастическими, в к-рых движение системы частиц (атомов, молекул) по пов-стям потенц. энергии дополняется учетом взаимод. системы с окружением, к-рое носит случайный (стохастический) характер из-за участия в нем большого числа частиц окружения. Мат. способ описания такого взаимод. - ф-ция корреляции случайной силы, действующей на систему со стороны окружения. Ф-ции м. б. независимо рассчитаны, напр., методами молекулярной динамики, использующими компьютерную симуляцию поведения большого числа частиц, или иногда определены экспериментально. В основе совр. теоретич. подхода лежит т. наз. обобщенное ур-ние Ланжевена, к-рое учитывает случайное действие окружения на выделенную систему частиц и обратную р-цию системы на окружение. При нек-рых упрощающих предположениях относительно взаимод. частиц внутри системы и взаимод. системы с окружением оказывается возможным построение целой иерархии приближений, к-рые формулируются в виде упрощающих ур-ний. К ним относятся ур-ние Фоккера - Планка (справедливо при условии, когда время "рассасывания" флуктуации в среде намного меньше характерных времен движения в системе), ур-ние Смолуховского (справедливо при том же предположении и при дополнит. условии установления почти равновесного распределения по скоростям частиц системы), диффузионное ур-ние Фика (справедливо при тех же предположениях и дополнит. условии своб. диффузии реагентов).
Химические реакция в сильных внешних полях - электрич., магн. и световых - сравнительно новое направление Д. э. а. В этих случаях наряду с взаимод. частиц между собой и с окружением приходится рассматривать их взаимод. с полями. Последние изменяют вероятности переходов; в частности, могут открываться новые пути превращений, к-рые в отсутствие полей запрещены. Возникает принципиальная возможность направленного влияния на элементарный акт воздействием внеш. излучения. Примером могут служить т. наз. радиационные столкновения, когда при сближении реагентов поглощается фотон, система переходит в новое электронное состояние, обладающее повышенной (и, возможно, направленной) реакц. способностью. Др. пример -влияние магн. полей на спиновые состояния частиц реагентов, от к-рых в решающей степени зависит эффективность элементарного акта (см. Магнитно-спиновые эффекты).