Однокомпонентные системы. Однокомпонентной системой является любое простое в-во или хим. соед., обладающее строго определенным составом в газообразном, жидком и твердом состояниях. Д. с. обычно строят на плоскости в координатах Т-р (рис. 1). Фазовые поля (области существования) пара V, жидкости L и твердой фазы S дивариантны, т.е. допускают одновременное изменение двух параметров состояния - Т и р.
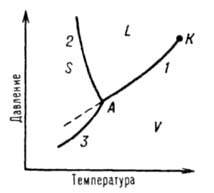
Рис. 1 Диаграмма состояния однокомпонентной системы. S, L и V - соотв. области существования твердой, жидкой и паровой фаз; 1, 2 и 3 кривые кипения (испарения), плавления и возгонки (сублимации) соотв., К критич. точка; А тройная точка.
Двухфазное равновесие между жидкостью и паром изображается кривой кипения (или испарения) 1, между жидкостью и
кристаллами - кривой плавления 2, между кристаллами и паром - кривой возгонки (или сублимации) 3. Все двухфазные равновесия моновариантны, т. е. не нарушаются при произвольном изменении только одного из параметров, Т или р; при этом значение другого определяется из Д. с. Кривая кипения 1 характеризует зависимость давления насыщенного пара в-ва от т-ры или зависимость т-ры кипения в-ва от внеш. давления. Со стороны повышенных T и р эта кривая заканчивается в критич. точке К, где исчезает различие в св-вах между жидкостью и ее паром (подробнее см. ст. Критическое состояние). Жидкость может находиться в переохлажденном состоянии (пунктирная линия на рис. 1). Аналогично кривая плавления характеризует зависимость т-ры плавления от внеш. давления, кривая возгонки - температурную зависимость давления насыщенного пара над твердым в-вом. На рис. 1 ход кривой плавления соответствует повышению т-ры плавления с ростом давления, однако возможно и понижение т-ры плавления с давлением (см. Клапейрона - Клаузиуса уравнение). Все три кривые моновариантных фазовых равновесий сходятся в тройной точке А, отвечающей параметрам состояния, при к-рых находятся в нонвариантном равновесии три фазы.
Д. с. усложняется, если в-во в твердом состоянии может существовать в разл. кристаллич. модификациях. Каждой модификации отвечает свое фазовое поле. Линии моновариантных равновесий, разграничивающие эти поля, наз. кривыми превращений.
Двойные системы.
Состояние двойной системы определяется тремя независимыми параметрами - Т, р и содержанием х одного из компонентов, поэтому Д. с. такой системы трехмерна. Обычно принимают постоянными Т или р и рассматривают соответствующие плоские сечения Д. с., называемые соотв.
изотермич. (р — х)или изобарными (Т — х)Д. с. В конденсир. системах роль давления сравнительно невелика и в качестве параметров состояния обычно выбирают Т и состав (концентрацию одного из компонентов).
Д и а г р а м м ы п л а в к о с т и. Такие Д. с. служат для установления условий равновесия между твердыми и жидкими фазами. Рассмотрим их осн. типы. Простейший вариант соответствует случаю, когда компоненты А и В образуют одну жидкую фазу (расплав или р-р), при охлаждении к-рой только выделяются (кристаллизуются) индивидуальные в-ва (не образуются ни твердые р-ры, ни хим. соед.).
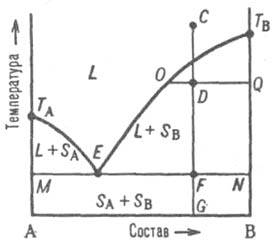
Рис. 2. Диаграмма плавкости двойной системы, компоненты к-рой А и В не образуют твердых р-ров. L - область существования жидкости (расплава), (L + SA) и (L + SB) области сосуществования жидкой фазы и твердых А и В соотв.; (SA + SB) область существования мех. смеси твердых А и В. ТАETВ и MEN - линии ликвидуса и солидуса соотв., E-эвтектич. точка. С, D, F, G, О и Q фигуративные точки (пояснения в тексте).
На Д. с. (рис. 2) линия, изображающая зависимость
от состава т-ры начала выделения из жидкой фазы твердого компонента (начала равновесной кристаллизации), наз. линией ликвидуса. Она состоит из двух ветвей ТАЕ и ТВЕ, отграничивающих фазовое поле жидкости L от полей сосуществования жидкой фазы с твердыми А и В соотв. (поля L + SA и L + SB). Линия, изображающая зависимость от состава т-ры окончания равновесной кристаллизации при охлаждении (или начала плавления при нагр.), наз. линией солидуса. Ниже нее расположено фазовое поле SA + SB твердого состояния системы, отвечающее условиям сосуществования двух твердых фаз.
Происходящие в системе фазовые изменения описываются след. образом. При охлаждении жидкой фазы, напр., из начального состояния С, фигуративная точка системы в целом движется вниз вдоль прямой CG. В точке ее пересечения с линией ликвидуса начинается кристаллизация компонента В, система становится двухфазной и дивариантной или, поскольку давление фиксировано, условно моновариантной. По мере кристаллизации В жидкость обогащается компонентом А, ее состав изменяется по ветви ликвидуса и по достижении системой состояния, изображаемого, напр., фигуративной точкой D, жидкой и твердой фазам соответствуют фигуративные точки О и Q. Прямые, соединяющие фигуративные точки двух находящихся в равновесии фаз, наз. нодами (или коннодами); горизонтальные ноды, подобные OQ, можно провести через любые точки фазовых полей, отвечающих гетерог. состояниям системы. При выражении состава в массовых (молярных) долях отношение отрезков OD и DQ пропорционально отношению масс (чисел молей) твердой и жидкой фаз (т. наз. правило рычага). Оно позволяет рассчитать по Д. с. относительные кол-ва фаз при любой т-ре, чтобы, напр., определить полноту кристаллизации или степень извлечения данного компонента из жидкой фазы в твердую.
В точке F пересечения прямой CG с линией солидуса начинается кристаллизация компонента А. Система становится трехфазной (жидкость и две твердые фазы А и В) и моновариантной (условно нонвариантной), т.е. при постоянном давлении совместная кристаллизация двух твердых фаз (т. наз. эвтектич. кристаллизация) протекает при постоянных т-ре и составе жидкой фазы, отвечающих координатам эвтектич. точки Е. После завершения эвтектич. кристаллизации система состоит из двух твердых фаз и является дивариантной (условно моновариантной). В обсуждаемом случае система после затвердевания состоит из относительно крупных кристаллов В и мелкодисперсной смеси совместно возникших при эвтектич. кристаллизации кристаллов А и В; такую смесь наз. эвтектикой. Если
исходная жидкость имела эвтектич. состав, продукт ее затвердевания - мелкодисперсная эвтектика без примеси крупных кристаллов к.-л. из компонентов. При нагр. смеси твердых А и В описанные явления протекают в обратной последовательности: изотермич. образование жидкости эвтектич. состава вплоть до исчерпания к.-л. из твердых компонентов и растворение в жидкости оставшегося твердого компонента при дальнейшем повышении т-ры, к-рое завершается по достижении фигуративной точкой системы линии ликвидуса.
Второй тип диаграммы характерен для случая ограниченной р-римости компонентов в твердом состоянии. Твердый р-р В в А (обозначается a-раствор) образуется лишь до определенной концентрации В, твердый р-р А в В (b-раствор) - лишь до определенной концентрации А. Для таких систем возможны два случая трехфазного равновесия: 1) эвтектич. равновесие жидкого расплава состава Е, твердого р-ра a, концентрация к-рого соответствует точке М, и твердого р-ра b, концентрация к-рого соответствует точке N, при эвтектич. т-ре, к-рая, как правило, ниже т-р плавления TA и ТB обоих компонентов (рис. 3).
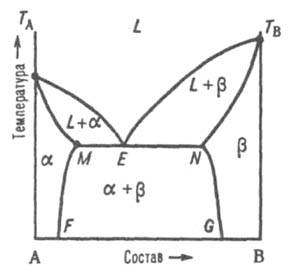
Рис. 3. Диаграмма плавкости двойной системы эвтектич. типа с ограниченными твердыми р-рами. L, a и b - области существования жидкой фазы (расплав) и твердых р-ров В в А и А в В соотв.; (L + a) и (L + b) - области сосуществования жидкой фазы и твердых р-ров a и b соотв.; (a + b) - область сосуществования двух твердых р-ров. ТАЕТВ и MEN - линии ликвидуса и солидуса соотв., E - эвтектич. точка.
При охлаждении затвердевшей смеси ниже линии солидуса MN происходит изменение концентраций твердых р-ров a и b соотв. по линиям MF и NG, к-рые дают температурную зависимость растворимости в твердом состоянии В в А и А в В. 2) Равновесие при т-ре Тр, к-рая является промежуточной между т-рами плавления ТА и ТB. Если, напр., т-ра начала кристаллизации расплава с высоким содержанием А выше ТА (рис. 4), а с высоким содержанием В - ниже ТB, линия ликвидуса состоит из двух ветвей ТАР и ТВР, соответствующих кристаллизации твердых р-ров a и b.
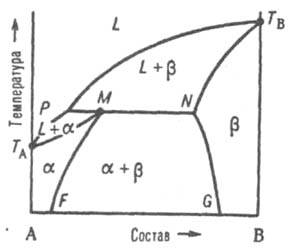
Рис. 4. Диаграмма плавкости двойной системы перитектич. типа. Р - перитектич. точка, остальные обозначения те же, что и на рис. 3.
Эти ветви пересекаются в т. наз. перитектич. точке Р - фигуративной точке жидкой фазы, к-рая может равновесно сосуществовать одновременно с двумя твердыми р-рами a и b, составы к-рых определяются точками М и N. Линия солидуса состоит из трех ветвей: ТAМ, MN и NTB. При охлаждении двухфазной системы (L + b) до перитектич. т-ры Тр в системе появляется третья фаза - р-р a. При протекании перитектич. превращения (фазовой р-ции) жидкость (расплав) + твердый р-р b D твердый р-р a система моновариантна, или условно нонвариантна, т. е. при данном давлении равновесие возможно лишь при постоянных т-ре и составах каждой из фаз. Если после окончания перитектич. р-ции остается избыток жидкой фазы, система переходит в двухфазное поле (L + a). При дальнейшем охлаждении происходит кристаллизация твердого a-раствора. Послед. понижение т-ры (ниже линии МF)
приводит к тому, что однородный твердый a-раствор становится неустойчивым и, распадаясь, выделяет нек-рое кол-во р-раствора, состав к-рого отвечает линии NG. Если после окончания перитектич. р-ции полностью исчезает жидкая фаза, система переходит в двухфазное поле a + b; по мере снижения т-ры составы a- и b-растворов изменяются в соответствии с ходом линий MF и NG.
Возможны и др. трехфазные равновесия, напр., при наличии у одного из компонентов полиморфных модификаций, когда все три сосуществующие фазы являются твердыми. Полиморфная модификация g может участвовать в т. наз. эвтектоидном превращении g D a + b или в перитектоидном превращении g + a D b, в принципе аналогичных рассмотренным выше эвтектич. и перитектич. превращениям. При метатектическом превращении модификация g при охлаждении распадается на твердую и жидкую фазы: g D a + L.
Третий тип диаграммы описывает состояния двойной системы, компоненты к-рой А и В образуют устойчивое хим. соед., к-рое не разлагается вплоть до т-ры плавления и переходит в жидкую фазу того же состава, т. е. плавится конгруэнтно.
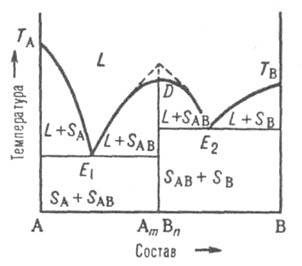
Рис. 5. Диаграмма плавкости двойной системы, компоненты к-рой А и В образуют конгруэнтно плавящееся хим. соед. АmВn. D - сингулярный максимум, Е1 и Е2 - эвтектич. точки; остальные обозначения те же, что и на рис. 3 и 4.
В точке плавления, соответствующей стехиометрич. составу АmВn, на линии ликвидуса имеется сингулярный максимум (рис. 5); это значит, что линия D - АmВn разделяет систему на две подсистемы. На диаграмме максимуму отвечает излом (показан пунктиром на рис. 5). В каждой из подсистем взаимод. между компонентами, соотв. А и АmВn, В и АmВn, может быть представлено диаграммами эвтектич. или перитектич. (или любого другого) типа. Если соед. AmBn частично диссоциировано в жидкой фазе, максимум на кривой ликвидуса несколько сглажен в соответствии со степенью диссоциации. Если соед. АmВn диссоциирует и в твердом состоянии, то сглаженный максимум будет и на линии солидуса. Однако независимо от вида максимума, общий характер фазового равновесия в системе определяется характером взаимод. соед. АmВn с компонентами А и В.
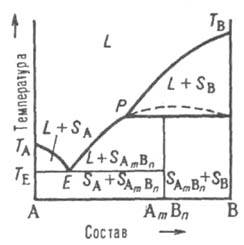
Рис. 6. Диаграмма плавкости двойной системы, компоненты к-рой А и В образуют инконгруэнтно плавящееся хим. соед. АmВn, обозначения те же. что и на рис. 4 и 5.
Четвертый тип диаграмм. Компоненты А и В образуют хим. соед., разлагающееся ниже т-ры плавления (т. наз. инконгруэнтное плавление). Напр., при охлаждении жидкости (расплава) до нек-рой т-ры Тр (рис. 6) кристаллизуется только компонент В; при Тр происходит перитектич. р-ция с образованием хим. соед. АmВn в твердом состоянии, т. е. р-ция твердая фаза SВ + расплав перитектич. состава D твердая фаза SА(m)В(n). Если при этом в твердой фазе компонент В имеется в избытке, в результате
перитектич. р-ции исчезает жидкая фаза и при дальнейшем охлаждении ниже Тр остается смесь двух твердых фаз SB и SА(m)B(n). Если же в твердой фазе компонента В недостает, в результате р-ции исчезают кристаллы В и жидкость при дальнейшем охлаждении выделяет кристаллы соед. АmВn, изменяя свой состав по линии ликвидуса РЕ. При т-ре ТЕ происходит эвтектич. кристаллизация AmBn и А. Возможны и др. варианты диаграммы. Описанные типы диаграмм плавкости могут усложняться из-за полиморфизма как компонентов А и В, так и соед. АmВn.
Диаграммы растворимости. При отсутствии в системе твердых фаз Д. с. состоит из области существования одной жидкой фазы (т. наз. области гомогенности) и области сосуществования двух насыщенных жидких р-ров разного состава, образующих несмешивающиеся друг с другом слои (рис. 7). Кривая, разделяющая эти области, наз. бинодалью. Так, при т-ре Т1 в равновесии находятся р-р компонента В в А (его состав отвечает точке С) и р-р А в В (его состав отвечает точке D). Если однородный р-р 1 охладить до т-ры Т1, он распадется на две жидкие фазы.
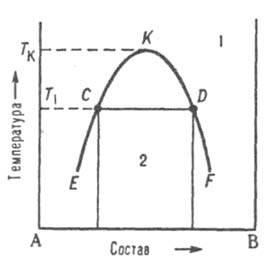
Рис. 7 Диаграмма растворимости двойной системы, компоненты к-рой А и В ограниченно растворимы друг в друге; 1 область существования однородного р-ра, 2 область сосуществования двух насыщенных р-ров; ECKDF - бинодаль, CD - нода, К -верхняя критич. точка растворимости.
Обычно при повышении т-ры взаимная растворимость жидкостей увеличивается, поэтому по своим св-вам оба насыщенных р-ра, составы к-рых изменяются по отрезкам бинодали ЕК и KF, сближаются. Наконец, при т-ре Tк различие между ними исчезает; эта т-ра наз. критической т-рой растворимости (смешения), выше нее может существовать лишь одна жидкая фаза. Большинство систем с расслоением р-ров характеризуются только одной критич. т-рой р-римости, чаще всего верхней, т. е. на Д. с. имеют незамкнутую снизу бинодаль. Если в таких системах не образуются хим. соед., область сосуществования двух жидких фаз ограничена снизу кривой кристаллизации одного из компонентов при т-ре превращения жидкая фаза 1 D жидкая фаза 2 + твердая фаза. Такое трехфазное равновесие наз. монотектическим; оно по своей термодинамич. природе аналогично эвтектическому или эвтектоидному. При синтектическом трехфазном равновесии две жидкие фазы взаимодействуют с образованием твердого соед. Такое равновесие аналогично перитектическому.
В нек-рых системах бинодаль имеет форму замкнутой кривой (овал), т. е. система имеет две т-ры смешения верхнюю и нижнюю.
Диаграмма равновесия жидкость-пар. При р = const каждому составу жидкой смеси отвечает определенная т-ра равновесия с паром и определенный состав пара, отличающийся, как правило, от состава жидкой смеси. На Д. с. (рис. 8, а) кривые кипения и конденсации изображают зависимости т-р начала кипения и конденсации от состава и отделяют поля жидкости L и пара V от поля (L + V)гетерог. состояний жидкость-пар. На кривой кипения м. б. экстремум: максимум (рис. 8, б) или минимум (рис. 8, в); в этих точках кривая кипения касается кривой конденсации, т. е. составы равновесных жидкости и пара совпадают Жидкие смеси такого состава полностью выкипают, подобно чистым жидкостям, при постоянной т-ре без изменения состава (см. Азеотропные смеси). Д. с., описывающие равновесия двухкомпонентных твердых р-ров с жидкими р-рами и жидких р-ров с паром, подобны.
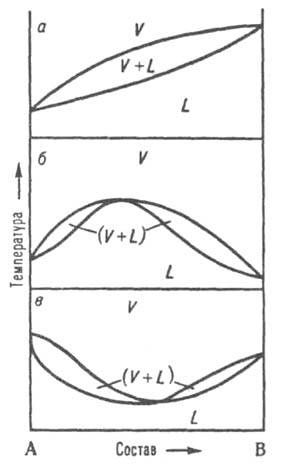
Рис. 8. Диаграммы состояния, двойной системы, описывающие равновесие жидкость - пар. L и V области существования жидкости и пара соотв.. (L + V) область сосуществования жидкой и паровой фаз; а система без азеотропной точки; б и в два типа азеотропных смесей
Тройные системы.
Состояния тройных систем однозначно определяются четырьмя независимыми параметрами: Т, р и молярными (массовыми) долями двух компонентов (доля третьего компонента определяется из условия равенства единице суммы долей всех компонентов). Поэтому при построении Д. с. тройных систем один из независимых параметров (р или Т) или два (р и T) фиксируют и рассматривают пространственные изобарные или изотермич. диаграммы или плоские изобарно-изотермич. диаграммы, соответствующие одному из сечений пространственной Д. с. Каждому составу тройной смеси отвечает определенная точка на плоскости составов. Область возможных составов тройных систем наз. композиционным треугольником или треугольником составов. В системе прямоугольных координат он представляет собой прямоугольный равнобедренный треугольник, вершины к-рого отвечают компонентам А, В и С, а стороны - двойным смесям АВ, ВС и СА. Более распространено использование равностороннего композиц. треугольника. В этом случае все компоненты равноправны, а за начало координат можно с равным основанием принять любую из его вершин (см. Многокомпонентные системы).
Для построения пространств. изобарной или изотермич. Д. с. по координатной оси, перпендикулярной композиц. треугольнику, откладывают соотв. T или р. При этом фигуративные точки системы в целом и ее трехкомпонентных фаз оказываются расположенными внутри трехгранной призмы, грани к-рой изображают двойные системы, ребра -однокомпонентные системы. На рис. 9, а изображена простейшая диаграмма плавкости тройной системы, компоненты к-рой А, В и С не образуют друг с другом твердых р-ров и (или) хим. соед. и не расслаиваются в жидком состоянии (неограниченно взаимно растворимы). Пов-сть т-р начала кристаллизации тройных расплавов (пов-сть ликвидуса) состоит из трех полей -ТAЕ1ЕЕ3, TBE1EE2 и ТCE2EE3, отвечающих кристаллизации А, В и С соотв. и разделенных тремя пограничными кривыми E1E, E2E и E3E. Ортогональные проекции пограничных линий на композиц. треугольник образуют т. наз. плоскую диаграмму плавкости тройной системы (рис. 9, б) с тремя полями кристаллизации компонентов AE1EE3, ВE1EE2, СE2EE3 Более полную информацию о системе дает плоская диаграмма с нанесенными на ней изотермами проекциями кривых пересечения пов-сти ликвидуса равноотстоящими плоскостями (рис. 9, в).
Рассмотрим с помощью Д. с. процессы, происходящие при охлаждении жидкого расплава, первоначальное состояние к-рого изображается, напр., фигуративной точкой М. Поскольку вертикальная прямая, проходящая через М, пересекает поле кристаллизации В (на плоской диаграмме проекция точки М находится в поле кристаллизации В), первым начинает кристаллизоваться именно этот компонент.
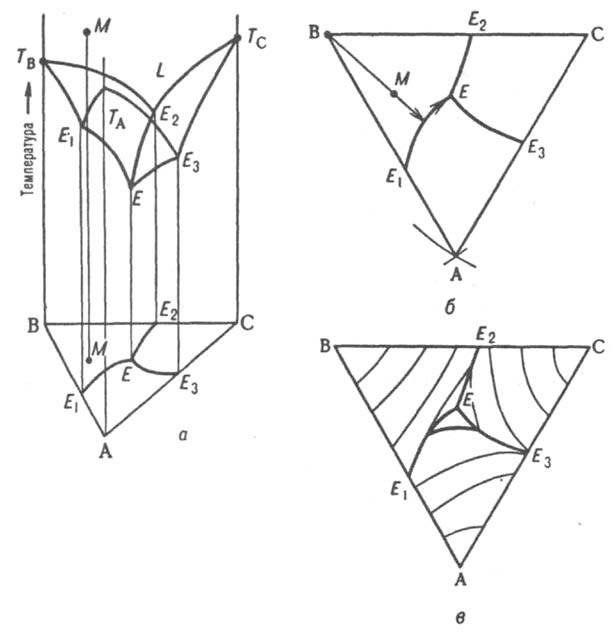
Рис. 9. Диаграмма плавкости тройной системы эвтектического типа: а - пространственная диаграмма, б плоская диаграмма, в плоская диаграмма с нанесенными на ней изотермами. ТА, ТB, ТC т-ры плавления компонентов А, В и С соотв., L область существования жидкой фазы; E1, E2, E3 эвтектич. точки двойных систем АВ, ВС и СА соотв., Е тройная эвтектич. точка; М фигуративная точка системы.
Первоначально однофазная и четырехвариантная (условно трехвариантная) система становится двухфазной и трехвариантной (условно дивариантной). Соотношение кол-в А и С в расплаве при кристаллизации В не изменяется, поэтому состав жидкости в ходе кристаллизации В изменяется вдоль прямой (луча кристаллизации), проходящей через точки М и В в направлении удаления от вершины В. В точке пересечения луча кристаллизации с пограничной кривой Е1Е начинает кристаллизоваться еще и А, система становится трехфазной (условно моновариантной). При дальнейшем охлаждении фигуративная точка жидкой фазы смещается вдоль пограничной линии Е1Е по направлению к тройной эвтектич. точке Е, в к-рой происходит кристаллизация всех трех компонентов при постоянной т-ре, завершающаяся полным затвердеванием системы. Эвтектич. т-ра отвечает условно нонвариантному равновесию всех четырех фаз. Кристаллизация тройной жидкой смеси любого состава в системе такого типа всегда заканчивается образованием тройной эвтектики, т. е. пов-стью солидуса рассматриваемой системы является горизонтальная плоскость, проходящая через точку Е.
Обычно рассматривают изотермич. сечение изобарной пространственной диаграммы, наз. изобарно-изотермической. Если при нек-рой т-ре все три компонента - жидкости, из к-рых две ограниченно смешиваются друг с другом, на Д. с., как и в случае двойных систем, имеется область сосуществования двух жидких фаз, ограниченная бинодалью ЕKF (рис. 10). Если жидким является лишь один из компонентов, напр., вода в системе, содержащей еще две соли В и С с общим ионом, диаграмма растворимости (рис. 11) состоит из четырех полей, отвечающих одной жидкой фазе L (поле ADEF), двухфазным состояниям (L + SВ) (поле DEB) и (L + SC) (поле FEC) с йодами, проходящими соотв. через точки В и С, и условно нонвариантному трехфазному состоянию (L+ SB + SС) (поле ВЕС), в к-ром твердые В и С находятся в равновесии с насыщенным этими в-вами р-ром состава Е, к-рый наз. эвтоническим; отвечающая ему фигуративная точка наз. эвтонической или эвтоникой.
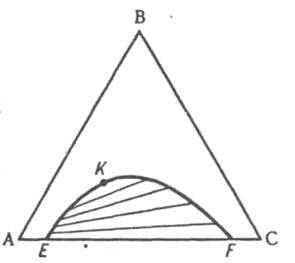
Рис. 10. Изобарно-изотермич. диаграмма состояния тройной системы ABC с ограниченной взаимной растворимостью компонентов А и С в жидком состоянии. EKF бинодаль, К - верхняя критич. точка растворимости.
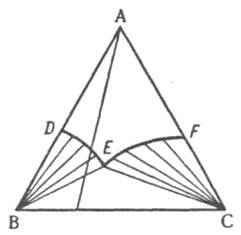
Рис. 11. Изобарно-изотермич. диаграмма растворимости твердых В и С в жидком растворителе A. DE и EF - линии растворимости (кристаллизации), Е - эвтонич точка (эвтоника).
Линии DE и FE - геометрич. место точек жидких фаз, находящихся в равновесии соотв. с твердыми В и С; они наз. линиями растворимости, или линиями кристаллизации, этих компонентов, т. к. в частном случае водных р-ров при изотермич. испарении воды, сопровождающемся движением фигуративной точки жидкости вдоль луча испарения, выходящего из вершины А, по достижении фигуративной точкой одной из этих линий начинается кристаллизация соответствующего компонента. При образовании в тройной системе хим. соед. (двойных солей, кристаллогидратов, интерметаллич. соед. и т. п.), а также твердых р-ров пространственные Д. с. и их плоские сечения усложняются. Для тройных водно-солевых систем, содержащих соли с общими ионами, при построении изобарно-изотермич. Д. с. по координатным осям (в прямоугольной системе координат) иногда откладывают не массовые или молярные доли компонентов, а молярные концентрации солей или молярную долю одной из солей в общей солевой массе и число молей воды на 100 молей солевой массы. Разработаны спец. методы построения Д. с. для тройных систем, между компонентами к-рых возможны р-ции замещения (обмена) или вытеснения, а также для систем, содержащих четыре и более компонентов. Лит.. Кауфман Л., Бернстейн Г., Расчет диаграмм состояния с помощью ЭВМ, пер. с англ., М., 1972; Аносов В. Я., Озерова М. И., Фиалков Ю. Я., Основы физико-химического анализа, М., 1976; Захаров А. М., Диаграммы состояний двойных и тройных систем, 2 изд., М., 1978; Новосёлова А. В., Методы исследования гетерогенных равновесий, М., 1980; Глазов В. М., Лазарев В. Б., Жаров В. В., Фазовые диаграммы простых веществ, М., 1980; Зломанов В. П., р-Т-х диаграммы двухкомпонентных систем, М., 1980; Петров Д. А., Двойные и тройные системы, М.. 1986. В. А. Михайлов.


