n2j = -r/ee0,
где n2-оператор Лапласа, e - диэлектрич. проницаемость р-рителя, e0 - электрич. постоянная (диэлектрич. проницаемость вакуума). Для каждого i-го сорта ионов r описывается ф-цией распределения Больцмана; тогда в приближении, рассматривающем ионы как точечные заряды (первое приближение Д.-Х.т.), решение ур-ния Пуассона принимает вид:
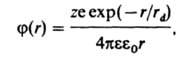
где z - зарядовое число центр. иона, rd - т. наз. дебаевский радиус экранирования (радиус ионной атмосферы). На расстояниях r > rd потенциал j становится пренебрежимо малым, т. е. ионная атмосфера экранирует электрич. поле центр. иона. Величина rd равна радиусу сферы, заряд к-рой равен заряду центр. иона и к-рая создает в месте нахождения центр. иона такой же потенциал, что и ионная атмосфера; значение rd выражается ф-лой:
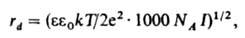
где k - постоянная Больцмана, Т - т-ра, NA - постоянная Авогадро, I - т. наз. ионная сила р-ра, зависящая от состава. Она определяется выражением:
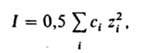
где сi - молярная концентрация i-го иона в моль/см3, zi - eгo зарядовое число; суммирование производится по всем типам ионов, присутствующих в р-ре. Д.-Х.т. дает возможность рассчитать средний ионный коэф. активности из выражения (предельный закон Дебая-Хюккеля):
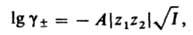
где коэф. А выражается ф-лой:
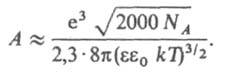
Для водных р-ров при 25°С А = 0,51. Согласно правилу Льюиса-Рендалла, коэф. активности данного типа ионов не зависит от типа др. присутствующих в р-ре ионов, а зависит только от ионной силы р-ра.
Д.-Х. т. широко используют для расчета коэф. активности ионов в разбавленных р-рах и концентрац. зависимости осмотич. коэффициентов. В первом приближении теория удовлетворительно описывает св-ва р-ров 1,1-валентных электролитов в области концентраций до 0,01 М, а для др. электролитов и неводных р-ров - в меньшем диапазоне концентраций. Введение поправок, учитывающих конечный размер ионов (второе приближение) и уменьшение e вблизи ионов (третье приближение), позволяет применять Д.-Х. т. в более широком диапазоне концентраций; для водных р-ров 1,1-валентных электролитов - до 0,1 М. Ур-ние для расчета коэф. активности в третьем приближении Д.-Х. т. имеет вид:
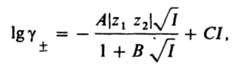
где В и С - эмпирич. постоянные. Ограниченность Д.-Х.т. обусловлена пренебрежением ассоциаций ионов, представлением о р-рителе как о непрерывной среде, характеризуемой только значением e, т. е. неучетом мол. структуры р-рителя и его взаимод. с ионами.
Д.-Х. т. является основой теории электропроводности разбавл. р-ров сильных электролитов, разработанной Л. Онсагером. Она позволяет объяснить увеличение электропроводности р-ра при повышении напряженности постоянного электрич. поля (эффект Вина) и в высокочастотном поле (эффект Дебая-Фалькенхагена). В этих условиях ионная атмосфера, тормозящая движение ионов, не успевает образоваться (см. Электропроводность электролитов).
Теория создана П. Дебаем и Э. Хюккелем в 1923.
Лит.: Робинсон Р., Стокc Р., Растворы электролитов, пер. с англ., М., 1963, с. 269-81; Измайлов Н. А., Электрохимия растворов, 3 изд., М., 1976, с. 68-89. А. И. Мишустин.


