Возмущений теория

ВОЗМУЩЕНИЙ ТЕОРИЯ в квантовой химии, метод приближенного описания сложной системы (атома, молекулы, кристалла) с помощью сведений о более простой системе, допускающей точное описание. В. т. количественно выражает интуитивно ясное представление о том, что малому изменению (т. наз. возмущению) простой (невозмущенной) системы отвечает малое изменение ее поведения. Напр., В. т. хорошо описывает изменение электронной плотности и реакц. способности ароматич. соед. при введении заместителей, потому что при этом само бензольное ядро изменяется мало. Формулы В. т. выражают решение ур-ния Шрёдингера для возмущенной молекулярной системы с оператором энергии (гамильтонианом) Н через решения ур-ния Шрёдингера для невозмущенной системы с гамильтонианом Н₀ и имеют вид разложений в ряд по степеням нек-рого вспомогат. параметра, характеризующего величину оператора возмущения V= H - Н₀. Ряды В. т. в принципе позволяют получить решение задачи с любой степенью точности, однако в приложениях ограничиваются обычно лишь первыми членами этих рядов, т. наз. низшими порядками В. т.

В квантовохим. задачах возмущениями считаются воздействия внеш. полей, влияние заместителей, электронно-колебат. взаимод. и др. Теорию применяют в осн. для решения след. задач.

1. Найти изменение волновых ф-ций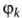 и отвечающих им энергий E_k стационарных состояний невозмущенной системы, удовлетворяющих ур-нию Шрёдингера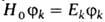 , под действием возмущения (задача о сдвиге уровней). Решение этой задачи применяют для анализа межмолекулярных взаимод., в теориях кристаллич. поля и поля лигандов, для изучения изменения молекулярных орбиталей при изменении строения молекул.

2. В момент времени t₀ возмущение отсутствует, система находится в состоянии с волновой ф-цией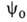. Требуется описать поведение системы при наличии возмущения в момент времени t > t₀ (задача об эволюции). Знание решения этой задачи требуется при анализе взаимод. молекул с излучением, при изучении динамики элементарного акта хим. р-ций; оно используется в теории дифракц. методов исследования строения молекул.

3. В момент времени t₀ молекулярная система находится в стационарном невозмущенном сост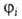оянии с волновой ф-цией и подвергается внеш. воздействию. Требуется определить вероятность найти систему в другом стационарном состоянии с волновой ф-цией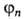после прекращения воздействия в момент времени t>t₀ (задача о вероятности перехода). Эта задача - частный случай задачи об эволюции, однако ее выделяют особо, поскольку она играет важную роль в изучении динамики элементарного акта хим. р-ции и в теории молекулярных спектров. В частности, решение этой задачи приводит к правилам отбора для квантовых переходов.

Различают стационарную и нестационарную (или временную) В. т. в зависимости от того, стационарное или нестационарное ур-ние Шрёдингера решается. Задачу о сдвиге уровней решают в рамках стационарной В. т. Стационарные волновые ф-ции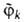 и отвечающие им энергии 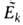возмущенной системы выражаются в первом порядке В. т. ф-лами:

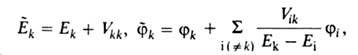
где V_ik-матричные элементы оператора возмущения. Поправка 2-го порядка для энергии E_k имеет вид:

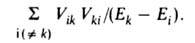
Приведенные выражения наз. ф-лами Рэлея - Шрёдингера. Они справедливы для невырожденного состояния невозмущенной системы с энергией E_k. Если же имеется вырождение энергетич. уровней, ф-лы усложняются. Напр., при Е_г = Е₂ = ... = Е_т поправки 1-го порядка к E_k находят как собств. значения матрицы с элементами V_kn (k, n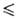т). Поэтому в общем случае вырождение по энергии под действием возмущения снимается; исключение - случай, когда возмущение одинаково действует на все вырожденные состояния, что, однако, встречается очень редко.

Задача об эволюции решается в рамках нестационарной В. т. Волновую ф-цию возмущенной системы записывают в виде:

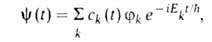
где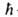 -постоянная Планка, i- мнимая единица, c_k(t)-зависящий от времени коэф., значение к-рого c^o_k в момент времени t₀ определено условием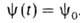 , В 1-м порядке В. т. c_k выражаются ф-лой:

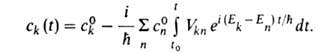
Эта ф-ла, полученная впервые П. Дираком и м. Борном, является также решением задачи о вероятности p_in перехода из состояния с волновой ф-цией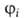в состояние с волновой 6-цией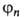, т. к. в этом случае с? = 1 и с_k = 0 при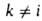, а

При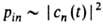 достаточно медленном (т. наз. адиабатическом) нарастании возмущения во времени стационарные состояния невозмущенной системы переходят в стационарные состояния возмущенной системы после окончания действия возмущения. Во всех случаях применение В. т. предполагает малость возмущения по сравнению с разностями энергетич. уровней невозмущенной системы.

Приведенные выше ф-лы справедливы для состояний дискретного спектра; в случае непрерывного спектра ф-лы модифицируются. Напр., число переходов р,у в единицу времени из состояния дискретного спектра с волновой ф-цией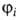 и энергией Е, в состояние непрерывного спектра с волновой ф-цией 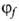и тем же значением энергии определяется т. наз. золотым правилом Ферми:

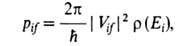
гд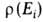е- плотность состояний, т. е. их число, приходящееся на единичный интервал энергии вблизи значения Е_i в непрерывном спектре.

Для получения надежных результатов с помощью В. т. важен физически обоснованный выбор невозмущенной системы и возмущения. В. т. применяют также в физике твердого тела, статистич. термодинамике (напр., для учета эффектов неидеальности) и др.

Лит.: Ландау Л. Д., Лившиц Е. М., Квантовая механика. Нерелятивистская теория, 3 изд., М., 1974 (Теоретическая физика, т. 3); Мессиа А., Квантовая механика, т. 2, пер. с франц., М., 1979, с. 181-253. В.И. Пупышев