Внутреннее вращение молекул

ВНУТРЕННЕЕ ВРАЩЕНИЕ МОЛЕКУЛ, вращение фрагментов молекулы относительно друг друга вокруг соединяющей их хим. связи. Обусловливает возникновение разл. конформаций молекулы, характеризуемых определенными значениями потенциальной энергии. Последняя меняется периодически при изменении угла относит. поворота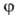 фрагментов молекулы (волчков) и описывается потенциальной ф-цией внутр. вращения (В. в.)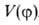. Максимумы потенциальных кривых (см. рис. 1) соответствуют нестабильным конформациям, минимумы - стабильным. Высота максимума по отношению к соседнему минимуму наз. потенциальным барьером В. в. V₀. В зависимости от соотношения значений V₀ и тепловой энергии молекул, равной kT (k-постоянная Больцмана, Т - абс. т-ра в К), различают своб. В. в., когда V₀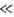k Т (напр., вращение метальных групп в СН₃С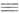ССН₃), и заторможенное В. в., когда V₀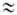kT (напр., в С₂Н_б, для к-рого V₀ = 12,5 кДж/моль). При V₀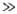kT В. в. отсутствует, как, напр., в молекуле СН₂=СН₂ при обычных т-рах. При своб. В. в. любые относит. ориентации вращающихся групп (т.е. все конформации) практически равновероятны. При заторможенном В. в. и его отсутствии существуют преим. стабильные конформации, причем в первом случае между ними осуществляются конформа-ционные переходы, а во втором нет. Появление потенциального барьера В. в. вокруг одинарной связи приближенно можно объяснить невалентными взаимод. атомов вращающихся фрагментов, природа к-рых та же, что и у межмолекулярного взаимодействия. Более строгое объяснение м. б. получено при квантовомех. рассмотрении с использованием неэмпирич. методов.

Число максимумов (и минимумов) потенциальной ф-ции В.в. для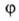 в пределах от 0 до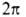(т.е. кратность барьера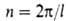 , где l-период ф-ции) зависит от природы атомов, связывающих вращающиеся фрагменты молекулы, числа и кратности образуемых каждым из этих атомов связей и от валентных углов. Так, для молекулы Н₂О₂ барьер двукратный, для С₂Н₆ - трехкратный, для CH₃BF₂-шестикратный. Чем выше порядок связи, вокруг к-рой происходит вращение, тем больше величина V₀. Общее выражение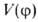 можно представить мат. рядом Фурье:

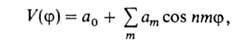
где а₀, a_m - коэф., т= 1,2,3... В случае симметричного трехкратного барьера (напр., когда волчок - группа СН₃, имеющая поворотную ось симметрии 3-го порядка С₃) п = 3, и при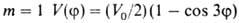 , т.е. 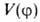описывает положение минимумов (V=0) и максимумов (V= V₀)потенциальной кривой; последующие члены ряда будут уточнять лишь ее форму (крутизну). Решение соответствующей квантовомех. задачи при заданном виде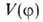в принципе позволяет найти набор энергетич. уровней для заторможенного В. в. Общий характер уровней энергии для трехкратного барьера показан на рис. 1.

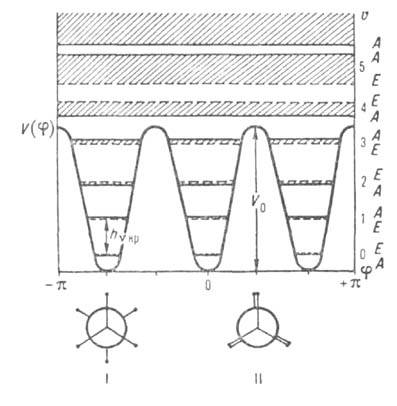
Рис. 1. Потенциальная ф-ция и уровни энергии заторможенного внутр. вращения для молекул, подобных этану. I-стабильные заторможенные (шахматные) конформации, II - заслоненные нестабильные конформации.

Термин "вращение" не является строгим и исчерпывающим. При высоких барьерах в ниж. части потенциальных ям система уровней энергии больше соответствует колебат. характеру движения и м. б. описана даже в приближении гармонического осциллятора: E(v) = hv_кр(v + 1/2), где v-колебат. квантовое число, v_кр - астота крутильного колебания (т.е. частота перехода; на рис. 1 показан стрелкой). Она связана с V₀ приближенной ф-лой: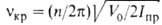 , где I_пр = (I₁I₂)/(I₁ +I₂) - приведенный момент инерции (I₁ и I₂-моменты инерции групп атомов, вращающихся одна относительно другой). Более строгое решение приводит к появлению полносимметричного А и вырожденного ? подуровней, относящихся к данному значению v, причем расщепление, показанное на рис. 1 заштрихованными областями, отражает вращат. характер внутримол. движения. При больших V₀ и малых v расщепление А-Е пренебрежимо мало, но по мере приближения к вершине барьера (увеличении v)это расщепление (или роль вращения) возрастает. Выше барьера расстояния между подуровнями А и Е с одним и тем же значением v становятся даже намного больше, чем между заштрихованными областями решений с разными v, т.е. полностью преобладает вращение. При V₀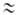О квантовомех. задача решается так же, как для своб. ротатора: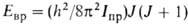, где J - вращательное квантовое число.

При отсутствии осевой симметрии волчков, напр. в молекулах 1,2-дизамещенных этана, заторможенное В. в. приводит к явлению поворотной изомерии, представляющей собой частный случай конформационной изомерии (см. Конформационный анализ), когда устойчивым конформациям соответствуют разные по глубине минимумы потенциальной энергии, т. е. возникают различающиеся по форме и св-вам поворотные изомеры (конформеры). В частности, у молекул типа 1,2-дизамещенных этана имеются три стабильных конформации - одна транс- (или анти-)и две гош-конформации (см. рис. 2). Относит. стабильность поворотных изомеров определяется разностью их энергий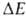, т.е. разностью значений энергии в минимумах потенциальной кривой. Напр., транс-изомер 1,2-дихлорэтана более устойчив, чем гош-изомер, т.к. его энергия (в газовой фазе) ниже на ~ 5,6 кДж/моль. При достаточно низких потенциальных барьерах (неск. десятков кДж/моль) поворотные изомеры находятся в термодинамич. равновесии, положение к-рого зависит от т-ры, давления и природы среды. Для барьеров порядка Ш кДж/моль время жизни конформеров составляет ~10^-10с. При высоких значениях V_Q (выше ~ 100 кДж/моль), когда В. в. отсутствует, конформеры даже при малой разности их энергий могут существовать как индивидуальные в-ва. В. в. молекул возможно в газовой и жидкой фазах, параметры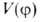 зависят от характера среды и электронного состояния молекулы. В кристаллах В. в., как правило, отсутствует и стабилен лишь один конформер; иногда существуют твердые фазы (напр., у некоторых фреонов), в которых стабильны разные конформеры и между ними осуществляются переходы.

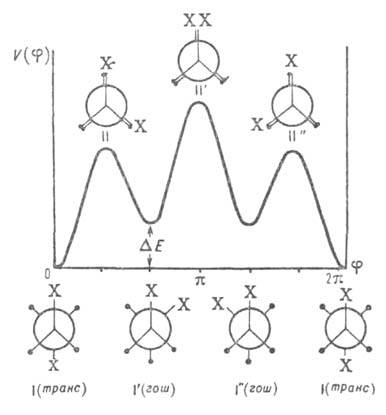
Рис. 2. Потенциальная ф-ция внутр. вращения молекул типа 1,2-дизамешенного этана. I-I''-поворотные изомеры (конформеры), или стабильные заторможенные конформации, II-II"-нестабильные заслоненные конформации.

Явления заторможенного В. в. и поворотной изомерии молекул оказывают влияние на термодинамич., электрич., оптич. и др. св-ва веществ. В. в. необходимо учитывать при расчете термодинамич. ф-ций методами статистич. термодинамики. Напр., для CH₃SH опытное значение энтропии 5^79 12 ⁼ 251,7 Дж/(моль*К), а расчетное (без учета В. в.) на 8,4 Дж/(моль*К) меньше. С др. стороны, если исходить из предположения о свободном В. в., расчетная величина S^o_279,12 превышает опытную на 2,0 Дж/(моль*К); следовательно, в молекуле CH₃SH существует заторможенное В. в. вокруг связи С—S.

В случае поворотной изомерии св-ва в-ва Определяются как св-ва равновесной смеси изомеров и зависят от внеш. условий, влияющих на положение равновесия. Напр., эффективный дипольный момент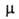 зависит от т-ры. Если 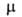поворотных изомеров различны, как, напр., у транс- ( 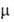= 0) и гош- 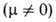конформеров 1,2-дихлорэтана, то при изменении т-ры значение измеряемого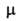будет приближаться к значению, характерному для изомера, концентрация к-рого будет при этом возрастать.В жидкой фазе и в среде полярных р-рителей повышается устойчивость более полярного гош-изомера в результате взаимод. молекул р-рителя и растворенного в-ва. Поворотные изомеры, имея разл. равновесные конфигурации, различаются своими колебат. и вращат. спектрами. При увеличении числа осей В. в. в молекуле возрастает и число ее возможных конформаций.

Представления, связанные с В. в. и поворотной изомерией молекул, применяют в теории строения как низкомол., так и высокомол. соединений. Разработаны методы и схемы конформационных расчетов достаточно сложных молекулярных систем на основе мех. моделей, получили также развитие полуэмпирич. и неэмпирич. квантовомех. расчеты потенциальных ф-ций В. в. молекул. Для изучения явлений В. в. и поворотной изомерии молекул используют методы спектроскопии: ИК, комбинац. рассеяния, микроволновой, УФ, ЯМР, ЭПР, а также методы газовой электронографии, поглощения ультразвука, некогерентного, неупругого рассеяния нейтронов, измерения дипольных моментов, диэлектрич. потерь и др.

Лит.: МидзусимаС, Строение молекул и внутреннее вращение, пер. с англ., М., 1957; Волькенштейн М.В., Конфигурационная статистика полимерных цепей, М.-Л., 1959; Пентин Ю. А., Вращательная изомерия молекул, М., 1969; Внутреннее вращение молекул, под ред. В.Дж. Орвилл-Томаса, пер. с англ., М., 1977. Ю.А. Пентин.