Валентных связей метод

ВАЛЕНТНЫХ СВЯЗЕЙ МЕТОД (метод валентных схем), метод приближенного решения электронного ур-ния Шрёдингера для многоэлектронных молекулярных систем. Основан на представлениях о двухцентровых хим. связях между атомами в молекуле, образуемых двумя электронами. Эти представления являются обобщением на многоатомные молекулы приближения Гайтлера - Лондона, позволившего впервые с помощью квантовомех. методов объяснить хим. связь в молекуле Н₂.

Осн. физ. идея В. с. м. состоит в том, что волновая ф-ция молекулы выражается через волновые ф-ции составляющих ее атомов. Образование хим. связи рассматривается как результат спаривания спинов своб. электронов атомов. Тем самым В. с. м. дает обоснование одному из осн. положений теории валентности: валентность нейтрального атома равна числу своб. электронов в его валентной оболочке. Каждому валентному штриху, соединяющему атомы А и В в структурной ф-ле молекулы, отвечает двухэлектронная ф-ция валентной связи Х_АВ(1,2), к-рая представляется в виде произведения двух волновых ф-ций: пространственной Ф(1,2), симметричной относительно перестановки координат электронов, и спиновой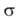(1,2), антисимметричной относительно такой перестановки и описывающей систему двух электронов с противоположными спинами; цифры 1 и 2 в этих обозначениях указывают пространств. координаты или спиновые переменные первого и второго электронов либо те и другие одновременно. Следовательно,

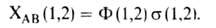
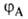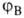Для простейшей молекулы Н₂ ф-цию Ф(1,2) строят из 1s-орбиталей атомов Н, обозначаемых для разных ядер как и, а ф-цию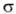(1,2) - из одноэлектронных спиновых ф-ци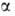йи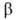(спин-функций), описывающих состояния электронов с противоположно направленными спинами:

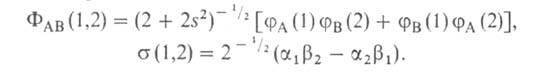
Энергия молекулы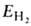, рассчитанная с такой двухэлектронной волновой ф-циеи Х(1,2), равна:

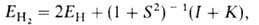
где Е_H-энергия атома Н,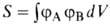 -интеграл перекрывания орбиталей (dV- элемент объема в пространстве координат одного электрона), I и К -т. наз. кулоновский и обменный интегралы соответственно. Кулоновский интеграл учитывает вклад в энергию связи, обусловленный электростатич. взаимод. неискаженных электронных облаков атомов между собой и с ядром соседнего атома, обменный - вклад, обусловленный деформацией электронного облака при образовании связи и перемещением его в пространство между ядрами (> 90% энергии связи); см. также Молекулярные интегралы.

Для более сложных молекул многоэлектронную волновую ф-цию представляют в виде антисимметризированного в соответствии с принципом Паули произведения всех двухэлектронных ф-ций типа Х_АВ(1,2) и ф-ций, описывающих состояние электронов внутр. оболочек, неподеленных электронных пар и неспаренных электронов, не занятых в двухцентровых связях. Отвечающее этой ф-ции распределение "валентных" штрихов, соединяющих атомы в молекуле, наз. валентной схемой. Такой подход наз. приближением идеального спаривания или приближением локализованных электронных пар. Электроны соотносят отдельным атомам и в соответствии с осн. идеей приближения Гайтлера - Лондона их состояния описывают атомными орбиталями. Согласно вариационному принципу (см. Вариационный метод), приближенную волновую ф-цию выбирают так, чтобы она давала миним. электронную энергию системы или, соответственно, наиб. значение энергии связи. Это условие, вообще говоря, достигается при наиб. перекрывании орбиталей, принадлежащих одной связи. Тем самым В. с. м. дает обоснование критерия макс. перекрывания орбиталей в теории направленных валентностей. Лучшему перекрыванию орбиталей, отвечающих данной валентной связи, способствует гибридизация атомных орбиталей, т.е. участие в связи не "чистых" s-, p-или d-орбиталей, а их линейных комбинаций, локализованных вдоль направлений хим. связей, образуемых данным атомом.

Внутриатомные вклады в энергию молекулы, аналогичные Е_Н, обычно превышают энергию своб. атомов на величину, называемую энергией промотирования. Такое превышение обусловлено электронной перестройкой атома при переходе его в валентное состояние, т.е. в состояние, требуемое для образования хим. связей, а именно: переходом электронов на энергетически менее выгодные атомные орбитали (напр., с 2s на 2р) при распаривании электронов, переходом от наиб. выгодных орбиталей в своб. атоме к менее выгодным гибридным орбиталям. Образование хим. связи объясняется тем, что выигрыш в энергии связи компенсирует затраты энергии на промотирование атомов.

Дальнейшее уточнение описания молекулярных систем в рамках В. с. м. связано с использованием линейных комбинаций волновых ф-ций неск. валентных схем. Такой подход обычно и наз. методом валентных схем. Коэффициенты в линейной комбинации ф-ций, отвечающих в приближении идеального спаривания разл. валентным схемам, возможным для данной молекулы, определяют вариационным методом. К валентным схемам относятся все схемы ковалентных (т. наз. кекулевских) структур с максимально возможным числом валентных связей между соседними атомами, т. наз. дьюаровских структур с "длинными" связями, в к-рых формально спарены электроны, принадлежащие несоседним атомам, а также структур ионного типа, в к-рых электрон формально перенесен от одного атома к другому. На этом основании В. с. м. нередко рассматривают как мат. обоснование теории резонанса. Один из простых способов построения всех валентных схем дается правилами Румера: каждой однократно занятой орбитали ставят в соответствие точку на нек-рой окружности, каждому спариванию электронов - стрелку, соединяющую две такие точки. Полученную диаграмму наз. диаграммой Румера. При построении полной волновой ф-ции молекулы учитывают все диаграммы Румера с непересекающимися стрелками. Диаграммы Румера дают удобный графич. метод вычисления матричных элементов гамильтониана на ф-циях валентных схем через кулоновские, обменные и др. интегралы. В полуэмпирич. вариантах В. с. м. кулоновские и обменные интегралы рассматривают как параметры, определяемые из спектроскопич. и термохим. данных, в неэмпирич. вариантах все молекулярные интегралы точно рассчитывают (см. Полуэмпирические методы, Неэмпирические методы).

Последоват. увеличение числа базисных атомных орбиталей и включение в расчет все большего числа валентных схем и электронных конфигураций позволяют получать практически точное неэмпирич. решение ур-ния Шрёдингера.

Достоинства В. с. м.- наглядность качеств. описания молекул с локализованными связями, непосредств. аналогия между валентными схемами и структурными ф-лами, возможность объяснения многих эмпирич. аддитивных закономерностей в химии. Однако этому методу часто предпочитают более простые по своей структуре молекулярных орбиталей методы.

Лит.: Пикок Т., .Электронные свойства ароматических и гетероциклических молекул, пер. с англ., М., 1969; Мак-Вини Р., Сатклиф Б., Квантовая механика молекул, пер. с англ., М., 1971 А. А. Багатурьянц.